Mesurer des inductances
Attention : But et intérêt du TP
Le but de ce TP est de proposer ou d'imaginer plusieurs méthodes permettant de mesurer la résistance et l'inductance propre d'une bobine d'induction.
La bobine choisie pourra être celle de la figure suivante.

La bobine est modélisée par le dipôle représenté sur la figure suivante.

La tension aux bornes de la bobine est :
\(u_L=L\frac{di}{dt}+ri\)
Le rôle d'une bobine d'auto-induction est de s'opposer à toute modification du courant dans un circuit (loi de Lenz).
En particulier, l'intensité du courant dans une bobine est nécessairement continue.
Méthode : Quels protocoles expérimentaux ?
On peut penser à différents montages vus en cours :
Utilisation directe d'un multimètre pour mesurer les valeurs de \(r\) et de \(L\).
Brancher un GBF (choisir un signal créneau) et réaliser un circuit série \((R+r,L)\)
Mesurer le temps nécessaire pour obtenir le régime permanent, relié à \(\tau=L/(r+R)\).
Mais comment mesurer indépendamment soit \(r\) soit \(L\) ?
On peut aussi tracer le diagramme de Bode du circuit série \((R+r,L\) et déterminer le gain maximum et la pulsation de coupure.
Fabriquer un circuit série \((R+r,L,C)\) et mesurer la tension aux bornes de \(R\) en choisissant un signal créneau.
La pseudo-période et le décrément logarithmique (donc le facteur de qualité) permettront de connaître les valeurs de \(L\) et de \(r\).

Fabriquer un circuit série \((R+r,L,C)\) et mesurer la tension aux bornes de \(R\) en régime sinusoïdal forcé.
L'étude de la résonance d'intensité permettra de connaître les valeurs de \(L\) et de \(r\).
Que vaut la pulsation de résonance et quel est le gain à la résonance ?
Complément : Utilisation d'un pont de mesures : le pont de Maxwell
Le pont de Maxwell est défini sur la figure suivante (c'est un cas particulier de pont de Wheastone).
(E) est un GBF utilisé en régime sinusoïdal forcé.
(D) peut être un ampèremètre branché avec une résistance de protection.

Le principe expérimental est d'équilibrer le pont, ce qui signifie annuler le courant dans la branche contenant le dipôle (D) en faisant varier les valeurs de \(C\) et de \(R\) (\(P\) et \(Q\) sont deux résistances fixes).
Notons \(\underline z_L=r+jL\omega\) l'impédance de la bobine et \(\underline y_C=1/\underline z_C=1/R+jC\omega\) l'admittance du condensateur en parallèle avec la résistance \(R\).
Soit \(\underline i_1\) le courant dans la bobine et la résistance \(Q\) et \(\underline i_2\) le courant dans la branche inférieure.
La tension aux bornes de (D) étant nulle :
\(\underline z_L \underline i_1=P\underline i_2\;\;\;\;et\;\;\;\;\underline z_C \underline i_2=Q\underline i_1\)
On en déduit :
\(\underline z_C \underline z_L=PQ\)
Soit :
\(\underline z_L=PQ\underline y_C\)
Ou encore :
\(r+jL\omega=PQ(\frac{1}{R}+jC\omega)\)
On identifie parties réelles et parties imaginaires :
\(L=PQC\;\;\;\;et\;\;\;\;r=\frac {PQ}{R}\)
Comment choisir les valeurs de \(P\) et de \(Q\) pour que, compte tenu des valeurs habituelles pour \(C\) et \(R\), on puisse mesurer correctement \(L\) et \(r\) ?
Complément : Diagramme de Fresnel
On réalise le montage suivant, alimenté par un GBF dont la fréquence sera de l'ordre de \(100\;Hz\).
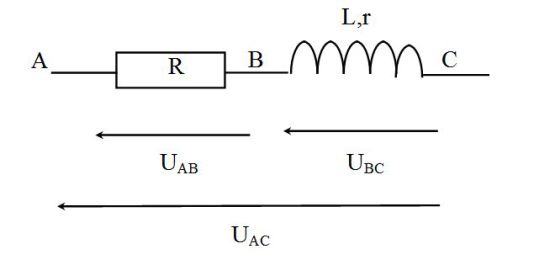
On mesure les tensions efficaces \(U_{AC}\), \(U_{BC}\) et \(U_{AB}\) avec un multimètre.
Tracer alors le diagramme de Fresnel du circuit (voir figure suivante).
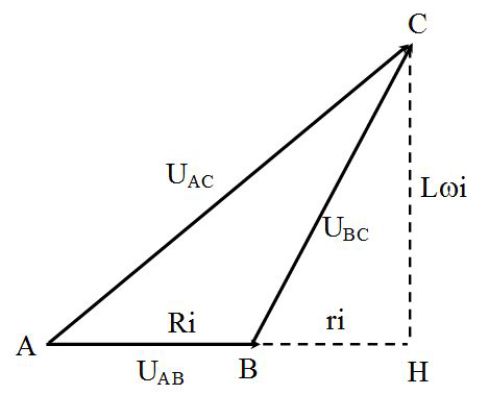
On peut alors en déduire les valeurs de \(L\) et de \(r\).
Par exemple, on peut écrire :
\(\frac{r}{R}=\frac{BH}{AB}\)
De même :
\(\frac{L\omega}{R}=\frac{HD}{AB}\)
Les distances \(AB\), \(BH\) et \(HD\) étant lues sur le diagramme de Fresnel.
Penser à évaluer les incertitudes.