Condensateur et pression électrostatique
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
On étudie un condensateur plan d'écartement d et ayant une différence de potentiel U entre ses deux armatures.
Question
Déterminer le champ électrostatique puis la capacité du condensateur.
Solution
On suppose que l'armature du bas a une charge Q et celle du haut – Q.
En négligeant les effets de bords, le plan du bas va créer un champ au dessus de lui :
\(\vec E = \frac{\sigma }{{2{\varepsilon _0}}}{\vec u_z} = \frac{Q}{{2S{\varepsilon _0}}}{\vec u_z}\)
Par superposition on trouve le champ :
\(\vec E = \frac{\sigma }{{{\varepsilon _0}}}{\vec u_z} = \frac{Q}{{S{\varepsilon _0}}}{\vec u_z}\)
On a :
\(V = - \int {\vec E \cdot \overrightarrow {dr} }\)
Donc :
\(U = \frac{{dQ}}{{S{\varepsilon _0}}}\)
D'où la capacité :
\(C = \frac{Q}{U} = \frac{{{\varepsilon _0}S}}{d}\)
Question
Calculer la pression électrostatique puis la force exercée sur l'une des armatures.
Solution
La pression électrostatique est :
\(P = \sigma \frac{{{{\vec E}_ + } + {{\vec E}_ - }}}{2} \cdot {\vec u_z} = - \frac{{{\sigma ^2}}}{{2{\varepsilon _0}}} = - \frac{{{Q^2}}}{{2{S^2}{\varepsilon _0}}}\)
Et la force vaut :
\(\overrightarrow F = - \frac{{{Q^2}}}{{2S{\varepsilon _0}}} \cdot {\vec u_z}\)
Question
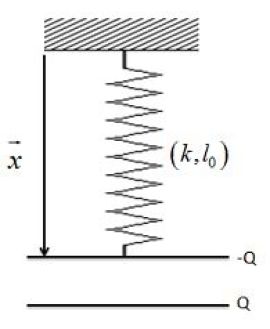
On accroche maintenant l'une des armatures par un ressort. On isole les deux armatures (leurs charges restent donc constantes).
Trouver l'écartement du condensateur à l'équilibre.
Solution
On écrit le PFD sur l'armature supérieure :
\(\ddot x + {\omega _0}\left( {x - {l_0} - \frac{{mg}}{k} - \frac{1}{k}\frac{{{Q^2}}}{{2S{\varepsilon _0}}}} \right) = 0\)
Où \({\omega _0} = \sqrt {\frac{k}{m}}\).
On en déduit :
\(x\left( t \right) = {l_0} + \frac{{mg}}{k} + \frac{1}{k}\frac{{{Q^2}}}{{2S{\varepsilon _0}}} + a\cos {\omega _0}t + b\sin {\omega _0}t\)
Les mouvements sont donc des oscillations autour de la positon d'équilibre :
\({x_{eq}} = {l_0} + \frac{{mg}}{k} + \frac{1}{k}\frac{{{Q^2}}}{{2S{\varepsilon _0}}}\)