Les condensateurs
Définition : Définition d'un condensateur
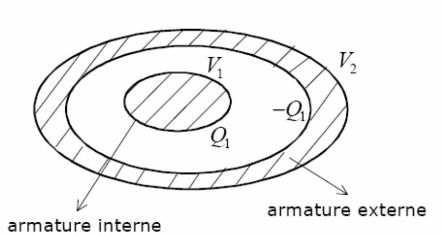
On appelle condensateur un système de deux conducteurs dont l'un est creux et entoure complètement l'autre.
L'espace séparant les deux armatures peut être vide ou rempli d'un isolant ("diélectrique").
Les faces en regard portent des charges opposées, notées \(Q_1\) et \(-Q_1\).
La capacité du condensateur est défini par :
\(C=\frac{Q_1}{V_1-V_2}\)
Méthode : Aspect énergétique, exemple du condensateur plan
En électricité, on a vu que l'énergie d'un condensateur pouvait s'écrire :
\(E_c=\frac{1}{2}Cu^2\)
où \(u\) est la tension aux bornes du condensateur.
Pour un condensateur plan, le champ électrique à l'intérieur des électrodes est uniforme et vaut :
\(E=\frac {\sigma}{\varepsilon_0}=\frac{q}{S\varepsilon_0}\)
La tension \(u\) est obtenue par la circulation du champ entre les deux électrodes, soit :
\(u=dE=\frac{qe}{S\varepsilon_0}\)
en notant \(e\) la distance entre les deux électrodes.
On retrouve ainsi la capacité d'un condensateur plan :
\(C=\frac{q}{u}=\frac{\varepsilon_0 S}{e}\)
On voit également que l'énergie du condensateur peut s'écrire :
\(E_c=\frac{1}{2}\frac{\varepsilon_0 S}{e} ({\frac{qe}{S\varepsilon_0}})^2\)
Soit :
\(E_c=\frac{1}{2}\varepsilon_0 E^2 (Se)\)
En remarquant que \(eS\) représente le volume entre les armatures, on retrouve l'expression de la densité volumique d'énergie ici purement électrique :
\(e_e=\frac{1}{2}\varepsilon_0 E^2 \)
L'expression de cette énergie est précisée dans le module de cours sur le bilan d'énergie électromagnétique.
Exemple : Calculs de capacités
Condensateur sphérique
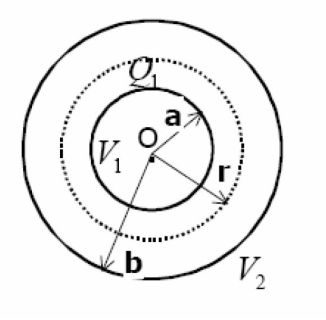
Les symétries et les invariances donnent :
\(\vec E=E(r)\vec e_r\)
Le théorème de Gauss appliqué à une sphère de centre O et de rayon \(r\) conduit à :
\(\vec E = \frac{Q_1}{4\pi \varepsilon_0 r^2} \vec e_r\)
Pour déterminer la différence de potentiel entre les armatures, on calcule la circulation du champ électrique entre les armatures :
\(V_1-V_2=\int_a^b\frac{Q_1}{4\pi \varepsilon_0 r^2} dr=\frac{Q_1}{4\pi \varepsilon_0 }(\frac{1}{a}-\frac{1}{b})\)
où \(a\) et \(b\) sont les rayons des deux électrodes (\(b>a\)).
On en déduit la capacité du condensateur sphérique :
\(C=4\pi \varepsilon_0 \frac{ab}{b-a}\)
Condensateur cylindrique
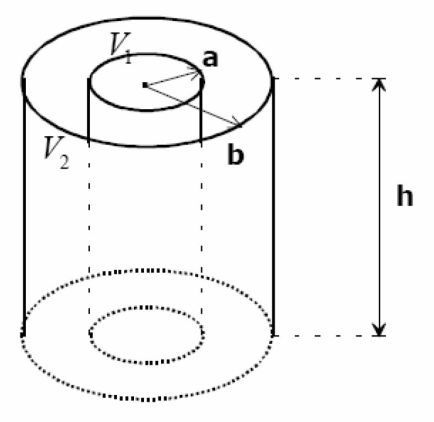
La méthode est identique à celle utilisée pour le condensateur sphérique.
Le champ électrique entre les électrodes est donné par le théorème de Gauss :
\(\vec E = \frac {Q_1}{2\pi \varepsilon_0 h r} \vec e_r\)
On calcule la circulation du champ entre les deux armatures :
\(V_1-V_2=\int_a^b\frac {Q_1}{2\pi \varepsilon_0 h r}dr=\frac{Q_1}{2\pi \varepsilon_0 h} ln(\frac{b}{a})\)
où \(a\) et \(b\) sont les rayons des armatures (\(b>a\)).
La capacité s'en déduit :
\(C=\frac{2\pi \varepsilon_0 h}{ln(b/a)}\)