Mouvements de particules chargées dans des champs électriques et magnétiques
Méthode : Champ électrique seul
On considère une particule chargée ponctuelle M (+ q) de masse m en mouvement dans un champ électrostatique \(\vec E_0\) uniforme et indépendant du temps.
Le référentiel d'étude est celui du laboratoire supposé galiléen.
Le PFD appliqué à la particule donne :
\(m\frac{{d\vec v}}{{dt}} = q\vec E\;\;\;\;\;soit\;\;\;\;\;\frac{{d\vec v}}{{dt}} = \frac{q}{m}\vec E\)
Il y analogie avec un point matériel dans le champ de pesanteur supposé uniforme :
\(m\frac{{d\vec v}}{{dt}} = m\vec g\;\;\;\;\;soit\;\;\;\;\;\frac{{d\vec v}}{{dt}} = \vec g\)
Par conséquent, le mouvement d'une particule dans le champ \(\vec E_0\) sera soit une droite soit une parabole.
Méthode : Champ magnétique seul
Puissance de la force magnétique :
On considère une particule chargée ponctuelle M (+ q) de masse m en mouvement dans un champ magnétostatique \(\vec B_0\) uniforme et indépendant du temps.
Le référentiel d'étude est celui du laboratoire.
Le PFD appliqué à la particule donne :
\(m\frac{{d\vec v}}{{dt}} = q\vec v \wedge \vec B\)
La puissance de la force magnétique est nulle (\(P = (q\vec v \wedge \vec B).\vec v = 0\)).
Par conséquent, d'après le théorème de la puissance cinétique :
\(P = \frac{{d{E_c}}}{{dt}} = 0\;\;\;\;\;soit\;\;\;\;{E_c} = cste\;\;\;\;et\;\;\;\;\;v = cste\)
Un champ magnétique ne modifie pas la norme de la vitesse mais seulement sa direction.
Mouvement circulaire :
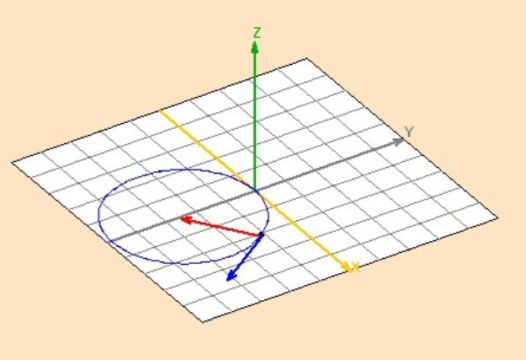
On considère une particule chargée ponctuelle M (+ q) de masse m en mouvement dans un champ magnétostatique \(\vec B_0=B_0\vec u_z\) uniforme et indépendant du temps.
La vitesse initiale de la particule est perpendiculaire au champ et portée, par exemple, selon l'axe (Ox) : \(\vec v_0=v_0 \vec u_x\).
Le PFD permet d'obtenir le rayon de la trajectoire (on suppose ici \(q>0\)) :
\(m\frac{v_0^2}{R}=qv_0B_0\)
Soit :
\(R=\frac{mv_0}{qB_0}\)
Ce cercle est parcouru à la vitesse angulaire constante :
\(\omega_0=\frac{v_0}{R}=\frac{qB_0}{m}\)
Mouvement hélicoïdal :
On considère une particule chargée ponctuelle M (+ q) de masse m en mouvement dans un champ magnétostatique \(\vec B_0=B_0\vec u_z\) uniforme et indépendant du temps.
La vitesse initiale de la particule est quelconque et peut s'écrire, par un choix convenable des axes :
\({\vec v_0} = {v_0 }\sin \alpha \;{\vec u_x}\; + \;{v_0 }\cos \alpha \;{\vec u_z}\)
La trajectoire dans le plan perpendiculaire à l'axe (Oz) est un cercle de rayon :
\(R=\frac{mv_0sin\alpha}{qB}\)
parcouru à la vitesse angulaire \(\omega_0\).
Le mouvement est rectiligne uniforme selon l'axe (Oz), à la vitesse \(v_0cos\alpha\vec u_z\).
La trajectoire est une hélice dont le pas est constant. Ce pas \(h\) vaut (c'est la distance parcourue pendant une période du mouvement circulaire dans le plan (Oxy)) :
\(h=\frac{2\pi}{\omega_0}v_0cos\alpha\)

Des vidéos illustrant divers mouvements :
Méthode : Champ électrique et champ magnétique
Hélice à pas variable :
On considère une particule chargée ponctuelle M (+ q) de masse m en mouvement dans un champ magnétostatique \(\vec B_0=B_0\vec u_z\) uniforme et indépendant du temps et dans un champ électrique \(\vec E_0=E_0\vec u_z\).
La vitesse initiale de la particule est quelconque et peut s'écrire, par un choix convenable des axes :
\({\vec v_0} = {v_0 }\sin \alpha \;{\vec u_x}\; + \;{v_0 }\cos \alpha \;{\vec u_z}\)
Le mouvement selon l'axe (Oz) est désormais accéléré :
\(z(t)=\frac{qE_0}{2m}t^2+v_0cos\alpha\)

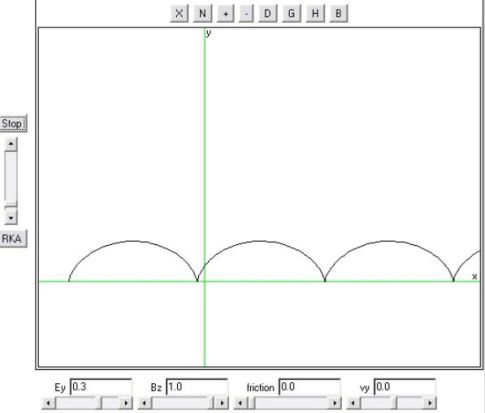
Cycloïde :
On considère une particule chargée ponctuelle M (+ q > 0) de masse m en mouvement dans un champ magnétostatique \(\vec B_0=B_0\vec u_z\) uniforme et indépendant du temps et dans un champ électrique \(\vec E_0=E_0\vec u_y\).
La particule est initialement à l'origine O du repère et sa vitesse initiale est nulle.
On posera :
\({\omega _c} = qB/m\)
Montrer que les équations paramétriques de la trajectoire sont :
\(x = \frac{E}{{B{\omega _c}}}({\omega _c}t - \sin {\omega _c}t)\;\;\;\;;\;\;\;\;y = \frac{E}{{B{\omega _c}}}(1 - \cos {\omega _c}t)\;\)
Une vidéo illustrant le mouvement d'une particule dans des champs électrique et magnétique croisés :


