Cinématique : changement de référentiel
Remarque : Relativité du référentiel
Le mouvement d'un mobile diffère selon le référentiel d'étude (relativité du mouvement).
Problématique :
On connaît le mouvement d'un point matériel dans un référentiel (R).
Quelle est la nature de ce mouvement, étudié dans un référentiel (R') en mouvement par rapport à (R) (trajectoire, vitesse et accélération) ?
Exemple :
Quelle est l'allure du mouvement de la Lune par rapport au Soleil ?
Simulation : Des animations JAVA de JJ.Rousseau (Université du Mans)
Méthode : Référentiels en translation l'un par rapport à l'autre
Un solide est animé d'un mouvement de translation si tous ses points possèdent à tout instant le même vecteur vitesse :
On peut donner l'exemple de la grande roue (translation circulaire) et du référentiel géocentrique (mouvement de translation quasi-circulaire par rapport au référentiel de Kepler).
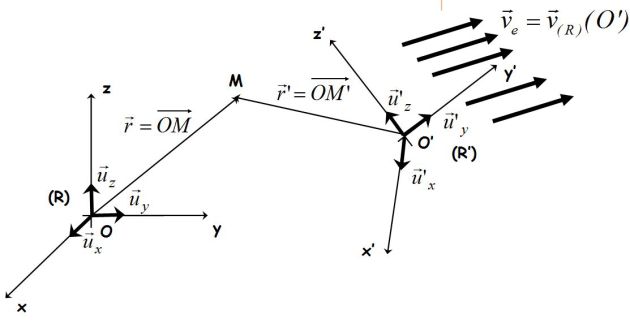
La figure suivante précise les notations.
Le référentiels (R'), d'axe (O'x'y'z') se déplace en bloc avec la vitesse d'ensemble qui est celle du point O' par rapport au référentiel (R).
On peut noter que les vecteurs de base de (R'), (\(\vec u'_x, \vec u'_y,\vec u'_z\)) gardent des directions fixes.
Loi de composition des vitesses :
La relation de Chasles donne :
\(\vec r = \overrightarrow {OM} = \overrightarrow {OO'} + \overrightarrow {O'M}\)
On calcule la vitesse dans (R) :
\({(\vec v)_R} = \vec v = {\left( {\frac{{d\overrightarrow {OM} }}{{dt}}} \right)_R} = {\left( {\frac{{d\overrightarrow {OO'} }}{{dt}}} \right)_R} + {\left( {\frac{{d\overrightarrow {O'M} }}{{dt}}} \right)_R}\)
L'indice (R) signifie que la vitesse \(\vec v\) est exprimée par rapport au référentiel (R), pour lequel les vecteurs de base \((\vec u_x, \vec u_y,\vec u_z)\) sont constants, mais pas les vecteurs \((\vec u'_x, \vec u'_y,\vec u'_z)\) , qui varient généralement au cours du temps.
Dans le cas d'un mouvement de translation, ces vecteurs sont constants et on obtient alors plus simplement :
\(\;{\left( {\frac{{d\overrightarrow {O'M} }}{{dt}}} \right)_R} = \;\frac{d}{{dt}}{\left( {x'\vec u{'_x} + y'\vec u{'_y} + z'\vec u{'_z}} \right)_R} = \dot x'\vec u{'_x} + \dot y'\vec u{'_y} + \dot z'\vec u{'_z} = \vec v'\)
Finalement : (loi de composition des vitesses)
\(\vec v(M) = \;\vec v'(M) + \vec v(O')\)
Loi de composition des accélérations :
De la même manière :
\(\vec a(M) = \;\vec a'(M) + \vec a(O')\)
On remarque que, pour une translation uniforme :
\(\vec a(M) = \;\vec a'(M)\)
Méthode : Référentiels en rotation pure l'un par rapport à l'autre
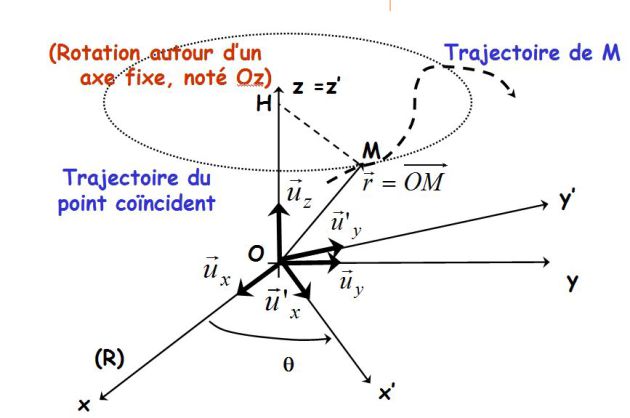
Le référentiel (R') est en rotation autour de l'axe (Oz) du référentiel "fixe" (R) (voir figure) :
On note :
\(\begin{array}{l}\vec r = \overrightarrow {OM} = x{{\vec u}_x} + y{{\vec u}_y} + z{{\vec u}_z} \\\;\;\;\;\;\;\;\;\;\;\; = x'\vec u{'_x} + y'\vec u{'_y} + z{{\vec u}_z} \\\end{array}\)
On note :
\(\theta = ({\vec u_x},\vec u{'_x})\;\;\;;\;\;\;\omega = \dot \theta \;\;\;et\;\;\;\vec \omega = \omega \;{\vec u_z}\)
\(\vec \omega\) est le vecteur vitesse angulaire de rotation du référentiel (R') par rapport au référentiel (R).
On peut rappeler que (voir cours de cinématique sur les dérivées de vecteurs tournants) :
\({\left( {\frac{{d\vec u{'_x}}}{{dt}}} \right)_R} = \dot \theta \;\vec u{'_y} = \;\omega \;\vec u{'_y}\;\;\;\;\;;\;\;\;\;\;{\left( {\frac{{d\vec u{'_y}}}{{dt}}} \right)_R} = - \dot \theta \;\vec u{'_x} = - \omega \;\vec u{'_x}\)
Loi de composition des vitesses :
On évalue :
\(\vec v = {\left( {\frac{{d\overrightarrow {OM} }}{{dt}}} \right)_R} = \frac{d}{{dt}}{\left( {x'\vec u{'_x} + y'\vec u{'_y} + z{{\vec u}_z}} \right)_R} = \vec v' + x'\frac{{d\vec u{'_x}}}{{dt}} + y'\frac{{d\vec u{'_y}}}{{dt}}\)
Soit :
\(\vec v = {\left( {\frac{{d\overrightarrow {OM} }}{{dt}}} \right)_R} = \vec v' + (x'\dot \theta \;\vec u{'_y} - y'\dot \theta \;\vec u{'_x})\)
Or :
\(\vec \omega \wedge \overrightarrow {OM} = \dot \theta \;{\vec u_z} \wedge (x'\vec u{'_x} + y'\vec u{'_y} + z{\vec u_z}) = (x'\dot \theta \vec u{'_y} - y'\dot \theta \vec u{'_x})\)
D'où la loi de composition des vecteurs vitesse :
\(\vec v = \vec v' + \vec \omega \wedge \overrightarrow {OM} = \vec v' + {\vec v_e}\;\;\;\;\;avec\;\;\;\;\;{\vec v_e} = \vec \omega \wedge \overrightarrow {OM}\)
Remarque : dérivation et changement de référentiel
\(\vec v = \vec v' + \vec \omega \wedge \overrightarrow {OM} \;\;\;\;\;soit\;\;\;\;\;{\left( {\frac{{d\overrightarrow {OM} }}{{dt}}} \right)_R} = \;{\left( {\frac{{d\overrightarrow {OM} }}{{dt}}} \right)_{R'}} + \vec \omega \wedge \overrightarrow {OM}\)
On peut généraliser cette formule au cas d'un vecteur \(\vec A\) quelconque : (formule de Varignon)
\({\left( {\frac{{d\vec A}}{{dt}}} \right)_R} = {\left( {\frac{{d\vec A}}{{dt}}} \right)_{R'}} + \vec \omega \wedge \vec A\)
C'est cette relation qui va être utilisée pour déterminer la loi de composition des vecteurs accélération.
Loi de composition des accélérations :
En utilisant la relation précédente :
\(\vec a = {\left( {\frac{{d\vec v}}{{dt}}} \right)_R} = {\left( {\frac{{d\vec v}}{{dt}}} \right)_{R'}} + \vec \omega \wedge \vec v\)
Puis :
\(\vec a = \frac{d}{{dt}}{\left( {\vec v' + \vec \omega \wedge \overrightarrow {OM} } \right)_{R'}} + \vec \omega \wedge \left( {\vec v' + \vec \omega \wedge \overrightarrow {OM} } \right)\)
\(\vec a = {\left( {\frac{{d\vec v'}}{{dt}}} \right)_{R'}} + {\left( {\frac{{d\vec \omega }}{{dt}}} \right)_{R'}} \wedge \overrightarrow {OM} + \vec \omega \wedge {\left( {\frac{{d\overrightarrow {OM} }}{{dt}}} \right)_{R'}} + \vec \omega \wedge \vec v' + \vec \omega \wedge \left( {\vec \omega \wedge \overrightarrow {OM} } \right)\)
Soit :
\(\vec a = \vec a' + \left( {\frac{{d\vec \omega }}{{dt}} \wedge \overrightarrow {OM} + \vec \omega \wedge \left( {\vec \omega \wedge \overrightarrow {OM} } \right)} \right) + 2\vec \omega \wedge \vec v'\)
On a ainsi : (loi de composition des accélérations)
L'accélération de Coriolis est nulle si le point M est au repos dans (R').
Cas d'une rotation uniforme (ω= cste) :
On évalue alors le seul terme :
\({\vec a_e} = \;\vec \omega \wedge \left( {\vec \omega \wedge \overrightarrow {OM} } \right)\)
Un rappel mathématique :
\(\vec a \wedge \left( {\vec b \wedge \vec c} \right) = (\vec a.\vec c)\;\vec b - (\vec a.\vec b)\;\vec c\)
Par conséquent :
\({\vec a_e} = (\;\vec \omega .\overrightarrow {OM} )\;\vec \omega - (\vec \omega .\vec \omega )\;\overrightarrow {OM} = (\;\vec \omega .\overrightarrow {OM} )\;\vec \omega - {\omega ^2}\;\overrightarrow {OM}\)
Soit H le projeté orthogonal de M sur l'axe (Oz) :
\(\vec \omega .\overrightarrow {OM} = \omega \;OH\)
D'où :
\({\vec a_e} = (\omega .OH)\;\vec \omega - {\omega ^2}\;\overrightarrow {OM} = {\omega ^2}(\overrightarrow {OH} - \overrightarrow {OM} ) = {\omega ^2}(\overrightarrow {OH} + \overrightarrow {MO} ) = {\omega ^2}\overrightarrow {MH}\)
Finalement :
\({\vec a_e} = - {\omega ^2}\overrightarrow {HM}\)
On retrouve l'expression de l'accélération pour un mouvement circulaire uniforme.