Le phénomène des marées océaniques (théorie statique des marées)
Fondamental :
La théorie statique des marées est une théorie simplifiée du phénomène des marées, dans laquelle la Terre est supposée immobile dans le référentiel géocentrique (Rg) (on néglige ainsi la rotation propre de la Terre ) et recouverte uniformément d'une couche d'eau au repos dans ce même référentiel.
La condition d'équilibre relatif de cette couche d'eau dans (Rg), prenant en compte les influences de la Lune et du Soleil (on néglige les influences des autres astres), fait apparaître des forces gravitationnelles différentielles, appelées forces génératrices des marées et responsables de celles-ci.
Le référentiel géocentrique (Rg) possède, par rapport au référentiel de Kepler (RK) supposé galiléen, un mouvement d'entraînement de translation quasi-circulaire ; il n'est donc pas galiléen et l'écriture des lois de Newton dans ce référentiel fait donc intervenir une force d'inertie d'entraînement.
Fondamental : Condition d'équilibre d'une masse d'eau
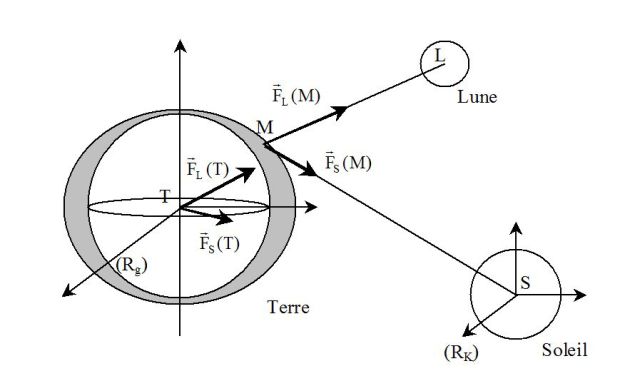
La condition d'équilibre d'une particule d'eau (supposée quasi-ponctuelle) de masse m située en un point M s'écrit, dans le référentiel géocentrique :
\(\left( {{{\vec f}_{pression}} - G\frac{{m{M_T}}}{{T{M^3}}}\mathop {TM}\limits^ \to } \right) - G\frac{{m{M_L}}}{{L{M^3}}}\mathop {LM}\limits^ \to - G\frac{{m{M_S}}}{{S{M^3}}}\mathop {SM}\limits^ \to + {\vec f_{ie}} = \vec 0\)
\(\vec f_{pression}\) désignent les forces de pression qui s'exercent sur la masse \(m\) ; \(M_T\), \(M_L\) et \(M_S\) sont les masses respectives de la Terre, de la Lune et du Soleil.
\(\vec f_{ie}\), force d'inertie d'entraînement, est donnée par :
\(f_{ie}=-m\vec a_e(M)\)
où \(\vec a_e(M)\) est l'accélération d'entraînement, au point M, du référentiel (Rg) par rapport au référentiel (RK).
Le mouvement d'entraînement étant un mouvement de translation, \(\vec a_e(M)\) s 'identifie à l'accélération, par rapport à (RK), d'un point quelconque de la Terre, par exemple le centre d'inertie T de celle-ci.
Cette accélération se détermine en appliquant le théorème du centre d'inertie à la Terre dans (RK) :
\(\begin{array}{l}{M_T}{{\vec a}_e} = - G\frac{{{M_T}{M_L}}}{{L{T^3}}}\mathop {LT}\limits^ \to - G\frac{{{M_T}{M_S}}}{{S{T^3}}}\mathop {ST}\limits^ \to \\{{\vec a}_e} = - G\frac{{{M_L}}}{{L{T^3}}}\mathop {LT}\limits^ \to - G\frac{{{M_S}}}{{S{T^3}}}\mathop {ST}\limits^ \to \\\end{array}\)
La condition d'équilibre de la masse m d'eau devient alors :
\(\left( {{{\vec f}_{pression}} - G\frac{{m{M_T}}}{{T{M^3}}}\mathop {TM}\limits^ \to } \right)+\left( { - G\frac{{m{M_L}}}{{L{M^3}}}\mathop {LM}\limits^ \to + G\frac{{m{M_L}}}{{L{T^3}}}\mathop {LT}\limits^ \to } \right) + \left( { - G\frac{{m{M_S}}}{{S{M^3}}}\mathop {SM}\limits^ \to + G\frac{{m{M_S}}}{{S{T^3}}}\mathop {ST}\limits^ \to } \right) = \vec 0\)
On note \(\vec F_{m,L}\) la quantité :
\({\vec F_{m,L}} = - G\frac{{m{M_L}}}{{L{M^3}}}\mathop {LM}\limits^ \to + G\frac{{m{M_L}}}{{L{T^3}}}\mathop {LT}\limits^ \to = {\vec F_L}(M) - {\vec F_L}(T)\)
où \(\vec F_L(M)\) et \(\vec F_L(M)\) sont les forces gravitationnelles exercées par la Lune sur une même masse m située soit en M soit en T (voir figure suivante).
Cette force, qui s'interprète comme une force différentielle de gravitation, peut encore s'écrire sous la forme :
\({\vec F_{m,L}} = m{\vec C_L}(M)\)
où \(\vec C_L(M)\) désigne le champ des marées dû à la Lune au point M, différence des champs gravitationnels créés par la Lune aux points M et T.
La force différentielle est appelée force génératrice des marées (due à l'influence de la Lune).
La force différentielle \(\vec F_{m,S}\) due à l'influence du Soleil sera de même : (voir figure précédente)
\({\vec F_{m,S}} = - G\frac{{m{M_S}}}{{S{M^3}}}\mathop {SM}\limits^ \to + G\frac{{m{M_S}}}{{S{T^3}}}\mathop {ST}\limits^ \to = {\vec F_S}(M) - {\vec F_S}(T)\)
Fondamental : Cas d'un seul astre attracteur
On ne considère dans ce paragraphe que l'influence d'un seul astre, la Lune par exemple.
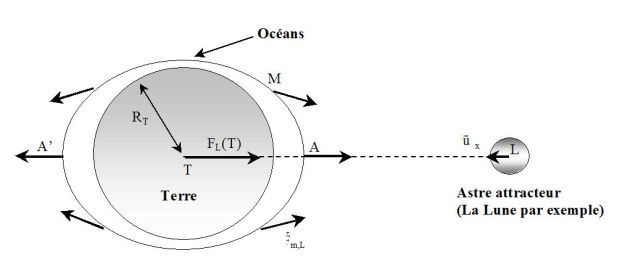
La figure suivante précise les directions des forces génératrices \(\vec F_{m,L}\) de la marée en différents points du globe terrestre.
On peut évaluer simplement la force génératrice aux points particuliers A et A', situés sur l'axe Terre–Lune.
En effet, au point A :
\({\vec F_{m,L}}(A) = Gm{M_L}\left( { - \frac{1}{{A{L^2}}} + \frac{1}{{T{L^2}}}} \right){\vec u_x}\)
où \(\vec u_x\) est le vecteur unitaire de l'axe (TL), dirigé de la Lune vers la Terre.
Soit RT le rayon terrestre et \(D_L=TL\) la distance Terre–Lune, alors, comme \(R_T<<D_L\) :
\(\frac{1}{{A{L^2}}} = \frac{1}{{{{({D_L} - {R_T})}^2}}} \approx \frac{1}{{D_L^2}}\left( {1 + 2\frac{{{R_T}}}{{{D_L}}}} \right)\)
Et, par conséquent, les expressions de la force puis du champ des marées en A deviennent :
\({\vec F_{m,L}}(A) = - 2\frac{{Gm{M_L}}}{{D_L^2}}\frac{{{R_T}}}{{{D_L}}}{\vec u_x} = m{\vec C_L}(A)\)
Avec :
\({\vec C_L}(A) = - 2\frac{{G{M_L}}}{{D_L^2}}\frac{{{R_T}}}{{{D_L}}}{\vec u_x}\)
Un calcul similaire conduit, au point A', à une force opposée :
\({\vec F_{m,L}}(A') = - {\vec F_{m,L}}(A)\)
L'effet de la marée est d'étirer principalement la surface des océans dans la direction de l'axe Terre–Lune et de donner ainsi au « bourrelet océanique » une forme à l'équilibre de « ballon de rugby ».
Le champ des marées, homogène à une accélération, peut s'exprimer en fonction du champ de pesanteur terrestre au sol g0, qui s'écrit, en négligeant la rotation propre de la Terre :
\({g_0} = G{M_T}/R_T^2\)
En particulier, aux points A et A', la norme du champ des marées est maximale et vaut ainsi :
\({C_{L,\max }} = {C_L}(A) = {C_L}(A') = 2\frac{{{M_L}}}{{{M_T}}}{\left( {\frac{{{R_T}}}{{{D_L}}}} \right)^3}{g_0}\)
Numériquement, avec \(R_T=6\;400\;km\), \(D_L=380\;000\;km\) et \(M_T/M_L=82\), on obtient :
\({C_L}(A) = {C_L}(A') = {1,2.10^{ - 7}}{g_0}\)
Seules des quantités gigantesques d'eau peuvent mettre en évidence l'existence de ce champ, beaucoup plus faible que g0.
Remarque :
Lorsque seule l'influence du Soleil est prise en compte, la valeur maximale du champ des marées est alors donnée par : (on donne \(M_S/M_T=3,30.10^5\))
\({C_{S,\max }} = 2\frac{{G{M_S}}}{{D_S^2}}\frac{{{R_T}}}{{{D_S}}} = 2\frac{{{M_S}}}{{{M_T}}}{\left( {\frac{{{R_T}}}{{{D_S}}}} \right)^3}{g_0}\)
où \(D_S=150.10^6\;km\) est la distance Terre-Soleil.
Numériquement, \({C_{S,\max }} = {5,1.10^{ - 8}}{g_0}\) et \({C_{L,\max }}/{C_{S,\max }} \approx 2,3\).
L'influence de la Lune (moins massive que le Soleil, mais plus proche de la Terre) sur les marées océaniques est plus importante que celle du Soleil.
Une vidéo sur le phénomène des marées océaniques
Complément : Existence de deux marées par jour
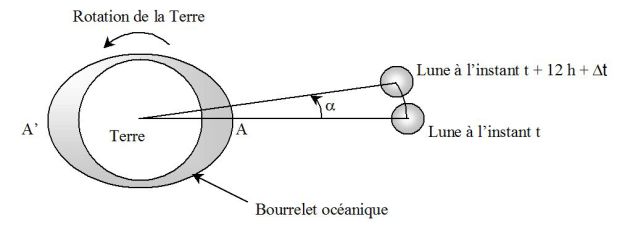
Si l'on prend en compte la rotation propre de la Terre dans le référentiel géocentrique, de période égale à pratiquement 24 h, le point A (voir figure) pour lequel à l'instant t la marée était haute se retrouvera de nouveau en marée haute au point A' lorsque la Terre aura effectué un demi-tour, c'est-à-dire au bout de 12 h.
On explique ainsi l'existence de deux marées hautes quotidiennes en un lieu donné.
Cependant, la Lune tournant autour de la Terre (sur une trajectoire supposée ici circulaire) avec une période de 27 jours 7 h (voir figure), le point A ne se retrouvera sur l'axe Terre–Lune qu'au bout de l'intervalle de temps 12 h + Δt, où Δt (exprimé en h) s'obtient en écrivant de deux manières différentes l'angle α défini sur la figure :
\(\alpha = \omega (12{\rm{ }} h + \Delta t) = \Omega \Delta t\)
où ω désigne la vitesse angulaire orbitale de la Lune autour de la Terre et Ω la vitesse angulaire de rotation propre de la Terre.
En supposant \(\Delta t<<12\;h\) :
\(\Delta t \approx 12\frac{\omega }{\Omega } = 0,44{\rm{ h = 26 min}}<<12\;h\)
Ainsi, l'écart temporel entre deux marées hautes successives en un même lieu est de l'ordre de 12 h 26 min alors que l'écart théorique entre une pleine mer et une basse mer sera de l'ordre de 6 h 13 min.
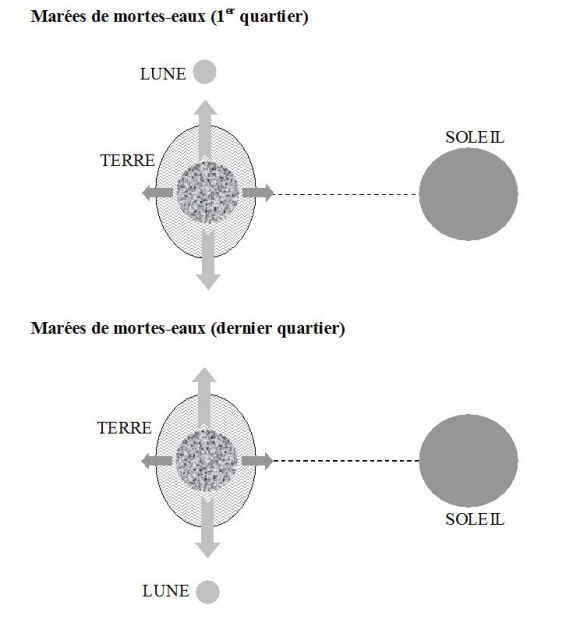
Complément : Marées de vives-eaux et de mortes-eaux
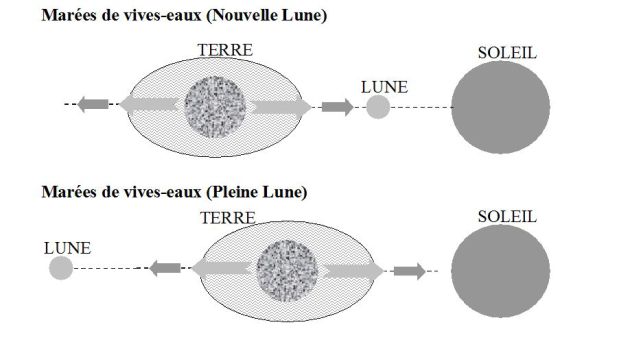
L'importance des variations de la hauteur d'eau (autrement dit, le marnage) induites par le phénomène des marées dépend notamment des positions relatives des trois astres, Terre, Lune et Soleil.
Lorsque les centres de ces trois astres sont alignés (et supposés être dans le plan de l'écliptique), c'est-à-dire lors de la nouvelle Lune ou de la pleine Lune (voir figure), les effets de marées provoqués par la Lune et le Soleil s'ajoutent, contribuant ainsi à un marnage important : les marées sont alors appelées marées de vives-eaux.
Par contre, lorsque les trois astres forment un angle droit (périodes correspondant au 1er ou au dernier quartier de la Lune), les forces de marées dues à la Lune et au Soleil se compensent en partie (celle due à la Lune restant prépondérante) : les marées correspondantes sont appelées marées de mortes-eaux.
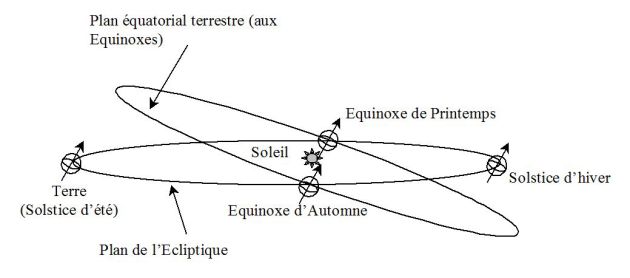
Complément : Marées d'équinoxes
Lors des équinoxes de mars et de septembre, le Soleil se trouve dans le plan de l'équateur terrestre (voir figure suivante) et renforce ainsi son effet de marée : les marnages deviennent importants et les coefficients de marée peuvent atteindre des valeurs allant jusqu'à 110, voir même 120 si l'équinoxe coïncide avec la Lune au périgée en nouvelle ou pleine Lune (cas des marées « du siècle »).
Par contre, lors des solstices de juin et de décembre, le Soleil est au plus loin du plan équatorial terrestre : l'effet du Soleil est moindre et les marées de vives-eaux sont alors moins importantes (les coefficients des marées de vives-eaux restent généralement inférieurs à 100).