Cinématique dans un référentiel
Attention : Vecteur vitesse
En coordonnées polaires :
\(\vec v = \dot r\;{\vec u_r}+r\dot \theta \;{\vec u_\theta }\)
En coordonnées cylindriques :
\(\vec v = \dot \rho {\vec u_\rho } + \rho \dot \theta {\vec u_\theta } +\dot z{\vec u_z}\)
En coordonnées sphériques :
\(\vec v = \dot r{\vec u_r} + r\dot \theta {\vec u_\theta } + r\sin \theta \dot \varphi {\vec u_\varphi }\)

Attention : Vecteur accélération
En coordonnées polaires :
\(\vec a = (\ddot r - r{\dot \theta ^2})\;{\vec u_r} + (r\ddot \theta + 2\dot r\dot \theta )\;{\vec u_\theta }\)
En coordonnées cylindriques :
\(\vec a = (\ddot \rho - \rho {\dot \theta ^2})\;{\vec u_\rho } + (\rho \ddot \theta + 2\dot \rho \dot \theta )\;{\vec u_\theta } + \;\ddot z\;{\vec u_z}\)
Exemple : Le mouvement circulaire
On note \(r=OM=R\) le rayon du cercle trajectoire.
Le vecteur vitesse angulaire du point \(M\) est :
\(\vec \omega = \omega \vec u_z = \dot \theta \vec u_z\)
où \(\theta\) est l'angle habituel défini en coordonnées polaires.
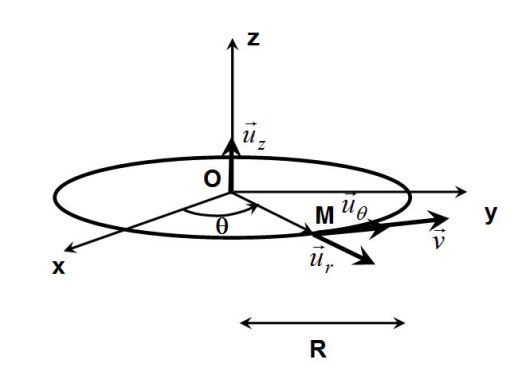
Le vecteur vitesse vaut :
\(\vec v=R \dot \theta \vec u_{\theta}\)
Le vecteur accélération vaut :
\(\vec a\; = \; - R{\dot \theta ^2}\;{\vec u_r}\; + \;R\ddot \theta \;{\vec u_\theta }\; = \; - \frac{{{v^2}}}{R}\;{\vec u_r}\; + \;R\dot \omega \;{\vec u_\theta }\)
Si le mouvement est uniforme (soit \(\omega = cste\)) :
\(\vec a\; = \; - \frac{{{v^2}}}{R}\;{\vec u_r}\;\)
L'accélération est purement centripète.
Des exemples de mouvements d'un point matériel :
