Analyse de Fourier
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Cet exercice n'est pas corrigé. Alors, n'hésitez pas à proposer vos solutions sur le forum.
(15 minutes de préparation)
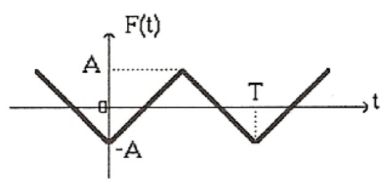
On donne le développement en séries de Fourier de la tension représentée sur la figure ci-dessous, de pulsation \(\omega=2\pi /T\) :
\(u_e (t) = - \frac{{8A}}{{\pi ^2 }}\left[ {\cos \omega t + \frac{1}{{3^2 }}\cos (3\omega t) + ... + \frac{1}{{(2k + 1)^2 }}\cos ((2k + 1)\omega t) + ...} \right]\)
On donne :
\(T=3,77\;ms\) et \(A=10,0\;V\).
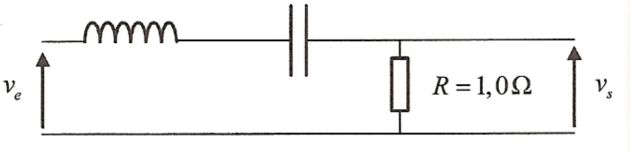
La tension \(u_e\) est injectée à l'entrée du filtre RLC ci-dessous.
Question
Calculer la fonction de transfert \(\underline H(j\omega)\) du filtre.
Quelle est sa pulsation de résonance \(\omega_0\) ? Que vaut son facteur de qualité \(Q\) ?
Comparer numériquement \(\omega_0\) à \(\omega\).
Indice
Utiliser la règle du diviseur de tension.
Quelle est la forme normalisée de ce filtre ?
Question
Préciser \(u_s(t)\) sous la forme d'une série de Fourier où l’amplitude complexe du terme de rang \(k\) sera donnée en fonction de \(A\), du module et de l'argument de la fonction \(\underline H\).
Indice
Le filtre est linéaire : la réponse est égale à la somme des réponses du fondamental et des harmoniques du signal triangulaire.
Question
Quel est le terme prépondérant dans cette série ?
Représenter sur le même schéma \(u_e(t)\) et \(u_s(t)\).
Quelle application peut-on imaginer à ce dispositif ?
Indice
Les harmoniques d'un signal triangulaire diminuent comme \(1/n^2\)