Modulation et démodulation
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
On considère le montage ci-dessous ; la tension d'entrée est ve(t)=V0sinωt.
On suppose que RC >> T = 2π/ω.
La diode est supposée idéale et de seuil nul.
On note v(t) la tension aux bornes de R.
Question
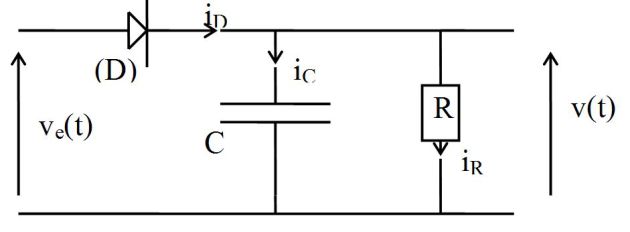
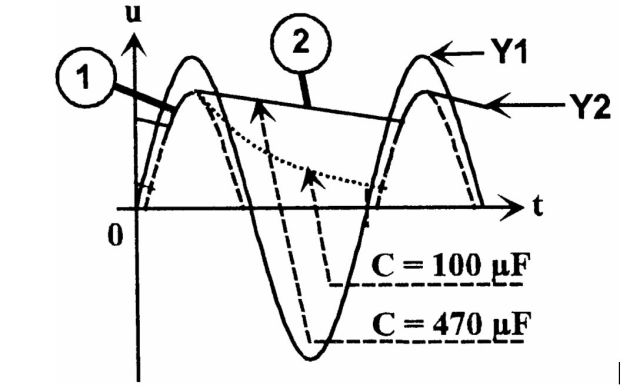
Décrire qualitativement et comparer les évolutions temporelles de ve(t) et v(t).
On pourra s'aider d'une représentation graphique.
Solution
L'allure de l'oscillogramme observé est donné sur la figure ci-dessous.
Question
A partir de quel instant t0 le courant iD dans la diode devient-il nul ? Montrer que v(t0) est alors pratiquement égale à V0.
Solution
On suppose la diode passante. Alors, \(v_e(t)=v(t)\). La loi des nœuds donne :
\({i_D} = {i_C} + {i_R} = C\frac{{dv}}{{dt}} + \frac{1}{R}v = C\omega \cos \omega t + \frac{1}{R}\sin \omega t = C\omega \left( {\cos \omega t + \frac{1}{{RC\omega }}\sin \omega t} \right)\)
Par conséquent :
\(\omega {t_0} \approx \frac{\pi }{2}\;et\;{t_0} \approx \frac{T}{4}\)
On a bien alors :
\(v({t_0}) \approx {V_0}\)
Question
Comment varie v(t) aux instants ultérieurs ?
Solution
La diode bloquée, le condensateur va se décharger lentement dans la résistance, selon la loi :
\(v(t) = {V_0}(1 - {e^{ - \frac{{t - {t_0}}}{\tau }}})\)
Question
Montrer qu'au cours d'une période, la variation maximale de tension Δv aux bornes de la résistance est approximativement proportionnelle à T et que Δv/V0 << 1.
Solution
Au bout d'une période T = t – t0 >> \(\tau\) :
\(v(t) = {V_0}(1 - {e^{ - T/\tau }}) \approx {V_0}(1 - \frac{T}{\tau })\)
Par conséquent :
\(\frac{{\Delta v}}{{{V_0}}} \approx \frac{T}{\tau } = \frac{T}{{RC}} < < 1\)
Question
AN : on désire que la tension v(t) soit de l'ordre de 12 V et qu'un courant de 1 mA circule dans R.
Quelle doit être la valeur de la capacité C pour que Δv/V0 < 10-2, la fréquence du générateur étant de 50 Hz ?