Filtrage linéaire
Définition :
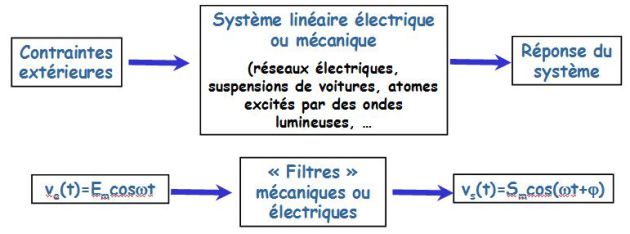
L'analyse harmonique (ou fréquentielle) d'un système est son étude au moyen de sa réponse harmonique \(s(t)\), c'est-à-dire de sa réponse en régime permanent sinusoïdal lorsqu'il est soumis à une entrée sinusoïdale \(e(t)\) dont on fait varier la pulsation \(\omega\).
Filtre du 1er ordre :
Exemple d'un filtre passe-bas :
\({\underline v _s}(t) = \underline H (j\omega ){\underline v _e}(t) = \frac{K}{{1 + j\omega \tau}}{\underline v _e}(t)\)
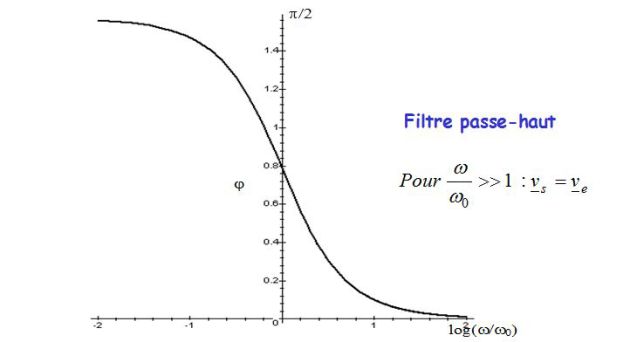
Exemple d'un filtre passe-haut :
\({\underline v _s}(t) = \underline H (j\omega ){\underline v _e}(t) = K\frac{j\omega \tau}{{1 + j\omega \tau}}{\underline v _e}(t)\)
\(\tau=1/\omega_c\), avec \(\omega_c\) la pulsation de coupure à \(-3\;dB\).
Filtre du 2nd ordre :
Exemple d'un filtre passe-bas :
\({\underline v _s}(t) = \underline H (j\omega ){\underline v _e}(t) = \frac{K}{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}} + 2j\sigma \frac{\omega }{{{\omega _0}}}}}{\underline v _e}(t)\)
où \(\omega_0\) est la pulsation propre du filtre et \(\sigma\) le coefficient d'amortissement.
On défini aussi le facteur de qualité \(Q=1/2\sigma\).
Exemple d'un filtre passe-haut :
\({\underline v _s}(t) = \underline H (j\omega ){\underline v _e}(t) = K\frac{\frac{{{\omega ^2}}}{{\omega _0^2}} }{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}} + 2j\sigma \frac{\omega }{{{\omega _0}}}}}{\underline v _e}(t)\)
Exemple d'un filtre passe-bande :
\({\underline v _s}(t) = \underline H (j\omega ){\underline v _e}(t) = K\frac{2j\sigma\frac{\omega}{\omega_0} }{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}} + 2j\sigma \frac{\omega }{{{\omega _0}}}}}{\underline v _e}(t)=\frac{K}{1+jQ(\frac{\omega}{\omega_0}-\frac{\omega_0}{\omega})}\)
\(\omega_0\) représente ici également la pulsation de résonance du filtre passe-bande.
Exemple d'un filtre réjecteur de bande (ou coupe-bande) :
\({\underline v _s}(t) = \underline H (j\omega ){\underline v _e}(t) = K\frac{1-\frac{{{\omega ^2}}}{{\omega _0^2}} }{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}} + 2j\sigma \frac{\omega }{{{\omega _0}}}}}{\underline v _e}(t)\)
Définition : Notations et définitions générales
On note :
\({\underline v _e}(t) = {V_{em}}{e^{j\omega t}}\;\;\;\;\;;\;\;\;\;\;\;{\underline v _s}(t) = {V_{sm}}{e^{j\varphi }}{e^{j\omega t}}\)
\(\varphi\) est le déphasage de la tension de sortie par rapport à la tension d'entrée du filtre.
\(\underline H(j\omega)\) est la fonction de transfert en tension du filtre :
\(\underline H (j\omega ) = \frac{{{{\underline v }_s}}}{{{{\underline v }_e}}} = \frac{{{V_{sm}}}}{{{V_{em}}}}{e^{j\varphi }}\)
Et :
\(G(\omega)\) est le gain réel :
\(G(\omega ) = \left| {\underline H (j\omega )} \right| = \frac{{{V_{sm}}}}{{{V_{em}}}}\)
\(G_{dB}\) est le gain en décibels (\(dB)\) :
\({G_{dB}}(\omega ) = 20\log G(\omega ) = 20\log \left( {\frac{{{V_{sm}}}}{{{V_{em}}}}} \right)\)
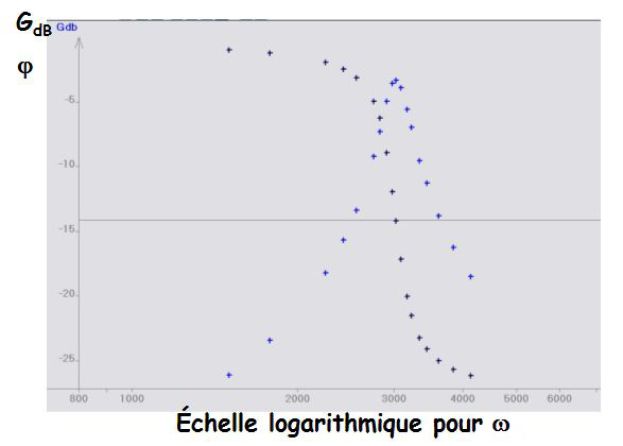
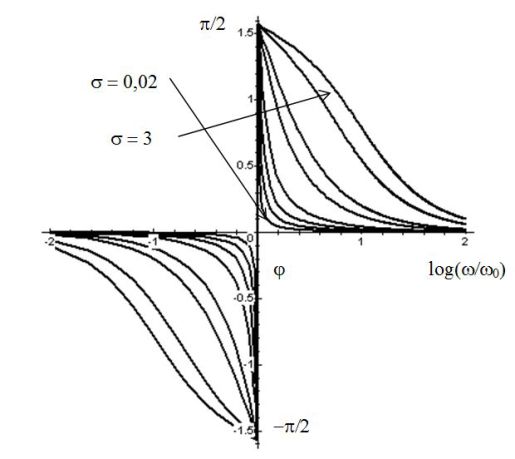
La figure précédente donne un diagramme de Bode d'un filtre passe-bande, c'est-à-dire la représentation graphique du gain en dB (\(G_{dB}(\omega)\)) et du déphasage \(\varphi(\omega)\) en fonction de la pulsation \(\omega\) et en échelle logarithmique.
Fondamental : Filtrage du 1er ordre (exemple du circuit RC série)
(Voir également la fiche expérimentale consacrée aux filtres du 1er ordre)
On étudie un circuit série RC et on mesure la tension de sortie \(\underline v_s\) en sortie ouverte.
Étude qualitative de la nature du flitre :
A basse fréquence, le condensateur est équivalent à un interrupteur ouvert (son impédance \(1/C\omega\) est infinie).
Le courant dans le circuit est nul. Ainsi, la tension aux bornes de R est nulle également et par conséquent \(\underline v_s=\underline v_e\).
A haute fréquence, le condensateur est équivalent à un fil de résistance nulle. Ainsi, \(\underline v_s=0\).
Le filtre étudié ici est donc un filtre passe-bas.
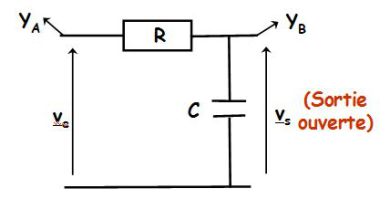
En sortie ouverte, la règle du diviseur de tension donne :
\({\underline v _s} = \frac{{\frac{1}{{jC\omega }}}}{{R + \frac{1}{{jC\omega }}}}{\underline v _e}\;\;\;\;\;soit\;\;\;\;\;\underline H (j\omega ) = \frac{{{{\underline v }_s}}}{{{{\underline v }_e}}} = \frac{1}{{1 + jRC\omega }} = \frac{1}{{1 + j\frac{\omega }{{{\omega _0}}}}}\)
Avec :
\(\omega_0=\frac{1}{RC}\)
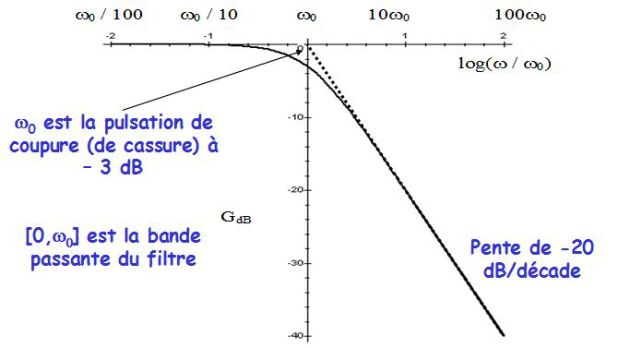
la pulsation propre du filtre, qui est aussi la pulsation de coupure à \(-3\;dB\), c'est-à-dire la pulsation pour laquelle le gain réel vaut \(G_{max}/\sqrt{2}\), ou, ce qui est équivalent, \(G_{dB}(\omega_0)=G_{dB,max}-3\;dB\).
C'est la fonction de transfert d'un filtre passe-bas du 1er ordre.
La figure précédente donne le diagramme de Bode en amplitude de ce filtre passe-bas du 1er ordre.
La figure suivante donne le diagramme de Bode en phase.
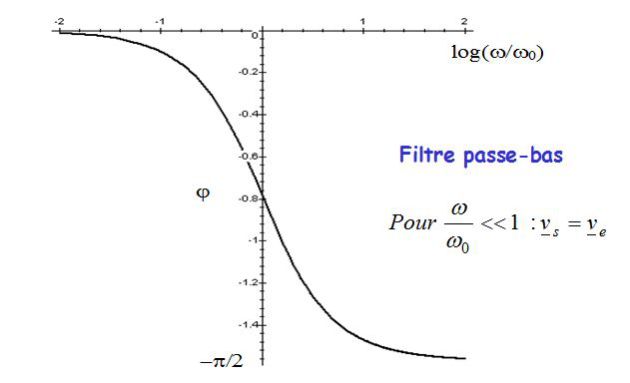
Autres filtres du 1er ordre :
Circuit série RC, tension de sortie aux bornes de R :
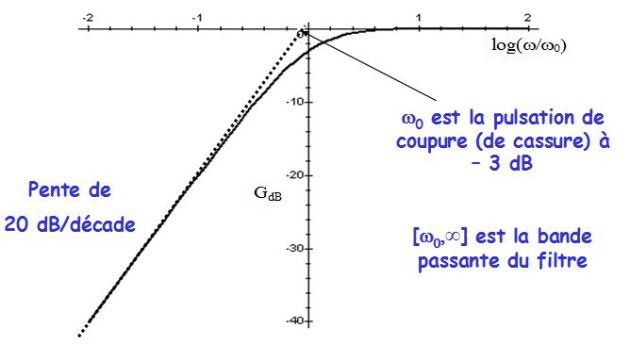
C'est un filtre passe-haut.
\(\underline H (j\omega ) = \frac{{{{\underline v }_s}}}{{{{\underline v }_e}}} = \frac{{j\frac{\omega }{{{\omega _0}}}}}{{1 + j\frac{\omega }{{{\omega _0}}}}} = \frac{1}{{1 - j\frac{{{\omega _0}}}{\omega }}}\)
Avec \(\omega_0=1/RC\).
Circuit série RL, tension de sortie aux bornes de L :
C'est un filtre passe-haut.
\(\underline H (j\omega ) = \frac{{{{\underline v }_s}}}{{{{\underline v }_e}}} = \frac{{j\frac{\omega }{{{\omega _0}}}}}{{1 + j\frac{\omega }{{{\omega _0}}}}} = \frac{1}{{1 - j\frac{{{\omega _0}}}{\omega }}}\)
Avec :
\(\omega_0=\frac{R}{L}\)
Circuit série RL, tension de sortie aux bornes de R :
C'est un filtre passe-bas.
\(\underline H (j\omega ) = \frac{{{{\underline v }_s}}}{{{{\underline v }_e}}} = \frac{1}{{1 + j\frac{\omega }{{{\omega _0}}}}}\)
Avec :
\(\omega_0=\frac{R}{L}\)
Les figures précédentes donnent le diagramme de Bode en amplitude et en phase d'un filtre passe-haut du 1er ordre.
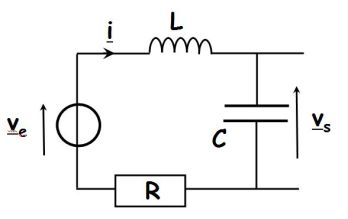
Fondamental : Filtrage du 2nd ordre (exemple du circuit RLC série)
Fondamental : Aux bornes de C en sortie ouverte : filtre passe – bas
La règle du diviseur de tension donne :
\(\underline H (j\omega ) = \frac{{\frac{1}{{jC\omega }}}}{{R + jL\omega \; + \frac{1}{{jC\omega }}}} = \frac{1}{{1 - LC{\omega ^2} + jRC\omega \;}}\)
On souhaite écrire cette fonction de transfert sous la forme normalisée :
\(\underline H (j\omega ) = \frac{K}{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}} + 2j\sigma \frac{\omega }{{{\omega _0}}}}}\)
Par identification :
\(\omega _0^2 = \frac{1}{{LC}}\;\;\;\;\;;\;\;\;\;\;jRC\omega = 2j\sigma \frac{\omega }{{{\omega _0}}}\;\;\;\;\;;\;\;\;\;\;K = 1\)
D'où :
\({\omega _0} = \frac{1}{{\sqrt {LC} }}\;\;\;\;\;;\;\;\;\;\;\sigma = \frac{1}{2}RC{\omega _0} = \frac{R}{2}\sqrt {\frac{C}{L}} \;\;\;\;\;;\;\;\;\;\;K = 1\)
Ainsi :
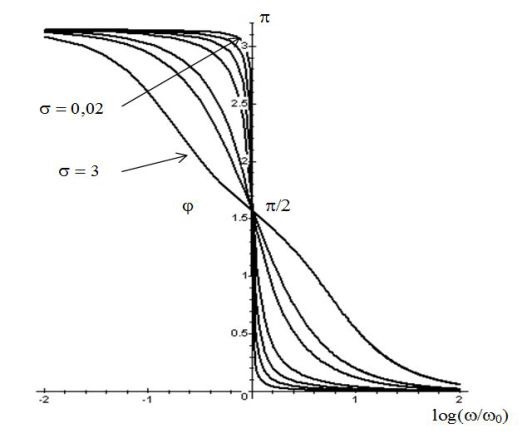
\(\underline H (j\omega ) = \frac{1}{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}} + 2j\sigma \frac{\omega }{{{\omega _0}}}}}\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;\;\left\{ \begin{array}{l}G(\omega ) = \frac{1}{{\sqrt {{{\left( {1 - \frac{{{\omega ^2}}}{{\omega _0^2}}} \right)}^2} + {{\left( {2\sigma \frac{\omega }{{{\omega _0}}}} \right)}^2}} }} \\\tan \varphi = - \frac{{2\sigma \frac{\omega }{{{\omega _0}}}}}{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}}}}\;\;\;(\sin \varphi < 0,\;\varphi \in \left[ { - \pi ,0} \right]) \\\end{array} \right.\)
En se référant à l'étude des oscillateurs mécaniques (réponse en élongation), on obtient :
Il y a "résonance de tension" aux bornes de C (« Résonance de charge »), c'est à dire correspondant à une tension aux bornes de C maximale, pour une pulsation \(\omega_r\) du GBF telle que :
\(\;\omega _r^{} = \omega _0^{}\sqrt {1 - 2{\sigma ^2}} \;\;\;\;\;\;\;\left( {avec\;\sigma < \frac{1}{{\sqrt 2 }}} \right)\)
Et la tension maximale aux bornes de C à la « résonance de charge » est :
\({V_{s,m}}({\omega _r}) = \frac{1}{{2\sigma \sqrt {1 - {\sigma ^2}} }}{V_{e,m}}\)
Les formules précédentes deviennent, en utilisant le facteur de qualité Q à la place du coefficient d'amortissement \(\sigma\) (\(Q=1/2\sigma\)) :
\(\;\omega _r^{} = \omega _0^{}\sqrt {1 - \frac{1}{{2{Q^2}}}} \;\;\;\;\;\;\;\;\;\;avec\;\;\;\;\;\;\;\;\;\;Q > \frac{1}{{\sqrt 2 }}\)
Et :
\({V_{s,m}}({\omega _r}) = \frac{Q}{{\sqrt {1 - \frac{1}{{4{Q^2}}}} }}{V_{e,m}}\)
Remarque :
Pour de faibles amortissements (\(\sigma\) «faible» et \(Q\) «grand»), alors :
\(\;\omega _r^{} \approx \omega _0^{}\;\;\;\;\;\;\;et\;\;\;\;\;\;\;{V_{s,m}}({\omega _r}) \approx Q{V_{e,m}}\)
Ainsi, si \(Q=10\), l'amplitude lors de la résonance vaut 10 fois celle de l'excitation : la résonance est dite «aiguë» et peut causer la destruction du système oscillant.
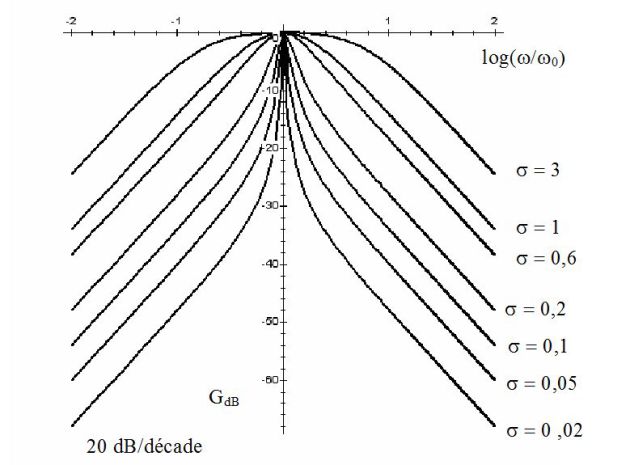
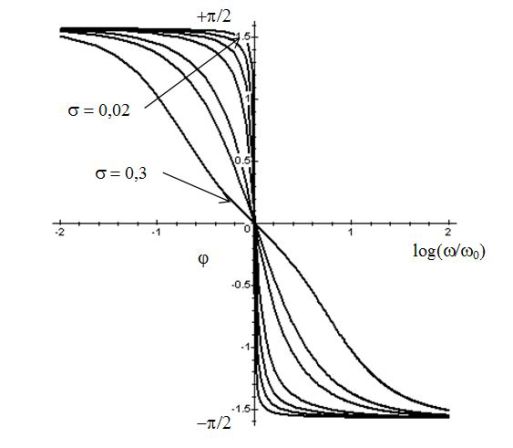
Les figures suivantes donnent le diagramme de Bode en gain et en phase d'un filtre passe-bas du 2nd ordre.
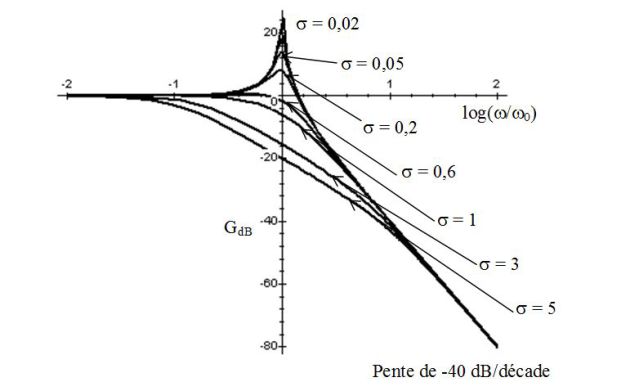

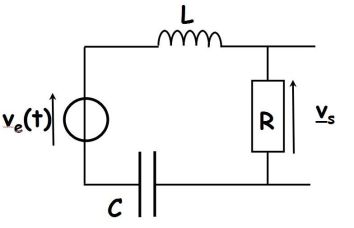
Fondamental : Aux bornes de R en sortie ouverte : filtre passe – bande
La règle du diviseur de tension donne :
\(\underline H (j\omega ) = \frac{R}{{R + jL\omega \; + \frac{1}{{jC\omega }}}} = \frac{1}{{1 + \frac{j}{R}\left( {L\omega \; - \frac{1}{{C\omega }}} \right)\;}}\)
On souhaite écrire cette fonction de transfert sous la forme normalisée :
\(\underline H (j\omega ) = \frac{{2j\sigma \frac{\omega }{{{\omega _0}}}}}{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}} + 2j\sigma \frac{\omega }{{{\omega _0}}}}}K = \frac{1}{{1 + \frac{j}{{2\sigma }}\left( {\frac{\omega }{{{\omega _0}}} - \frac{{{\omega _0}}}{\omega }} \right)}}K\)
Par identification :
\(\frac{L}{R} = \frac{1}{{2\sigma {\omega _0}}}\;\;\;\;\;;\;\;\;\;\;\frac{1}{{RC}} = \frac{{{\omega _0}}}{{2\sigma }}\;\;\;\;\;;\;\;\;\;\;K = 1\)
D'où (rapport membres à membres) :
\(\omega _0^2 = \frac{1}{{LC}}\;\;\;\;\;;\;\;\;\;\;\sigma = \frac{R}{2}\sqrt {\frac{C}{L}} \;\;\;\;;\;\;\;\;\;K = 1\)
Ainsi :
\(\underline H (j\omega ) = \frac{{2j\sigma \frac{\omega }{{{\omega _0}}}}}{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}} + 2j\sigma \frac{\omega }{{{\omega _0}}}}} = \frac{1}{{1 + \frac{j}{{2\sigma }}\left( {\frac{\omega }{{{\omega _0}}} - \frac{{{\omega _0}}}{\omega }} \right)}}\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;\left\{ \begin{array}{l}G(\omega ) = \frac{1}{{\sqrt {1 + \frac{1}{{4{\sigma ^2}}}{{\left( {\frac{\omega }{{{\omega _0}}} - \frac{{{\omega _0}}}{\omega }} \right)}^2}} }} \\\tan \varphi = - \frac{1}{{2\sigma }}\;\left( {\frac{\omega }{{{\omega _0}}} - \frac{{{\omega _0}}}{\omega }} \right)\;\;(\cos \varphi > 0,\;\varphi \in \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]) \\\end{array} \right.\)
Résonance de tension aux bornes de R (« résonance d'intensité ») :
Il y a "résonance de tension" aux bornes de R (« résonance d'intensité »), correspondant à une tension aux bornes de R maximale, pour une pulsation du GBF égale à la pulsation propre \(\omega_0\) du circuit (RLC) série :
\(\;{\omega _0} = \frac{1}{{\sqrt {LC} }}\)
Et la tension maximale aux bornes de R à la « résonance d'intensité » est :
\({V_{s,m}} = {V_{e,m}}\)
La bande passante vaut :
\(\Delta \omega = {\omega _{{c_2}}} - {\omega _{{c_1}}} = \frac{R}{L}\;\;\;\;\;\;\;\;\;;\;\;\;\;\;\;\;\;\;\;\Delta \omega = 2\sigma {\omega _0} = \frac{{{\omega _0}}}{Q}\)
Les figures suivantes donnent le diagramme de Bode en gain et en phase d'un filtre passe-bande du 2nd ordre.
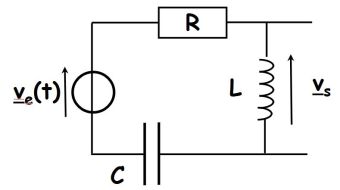
Fondamental : Aux bornes de L en sortie ouverte : filtre passe – haut
La règle du diviseur de tension donne :
\(\underline H (j\omega ) = \frac{{jL\omega }}{{R + \;jL\omega + \frac{1}{{jC\omega }}}} = \frac{{ - LC{\omega ^2}}}{{1 - LC{\omega ^2} + jRC\omega \;}}\)
On souhaite écrire cette fonction de transfert sous la forme normalisée :
\(\underline H (j\omega ) = \frac{{\left( { - \frac{{{\omega ^2}}}{{\omega _0^2}}} \right)}}{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}} + 2j\sigma \frac{\omega }{{{\omega _0}}}}}K\)
Par identification, on retrouve les mêmes caractéristiques :
\({\omega _0} = \frac{1}{{\sqrt {LC} }}\;\;\;\;\;;\;\;\;\;\;\sigma = \frac{1}{2}RC{\omega _0} = \frac{R}{2}\sqrt {\frac{C}{L}} \;\;\;\;\;;\;\;\;\;\;K = 1\)
Ainsi :
\(\underline H (j\omega ) = \frac{{\left( { - \frac{{{\omega ^2}}}{{\omega _0^2}}} \right)}}{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}} + 2j\sigma \frac{\omega }{{{\omega _0}}}}}\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;\left\{ \begin{array}{l}G(\omega ) = \frac{{\left( {\frac{{{\omega ^2}}}{{\omega _0^2}}} \right)}}{{\sqrt {{{\left( {1 - \frac{{{\omega ^2}}}{{\omega _0^2}}} \right)}^2} + 4{\sigma ^2}{{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^2}} }} \\{\varphi _{passe - haut}} = {\varphi _{passe - bas}} + \pi \\\end{array} \right.\)
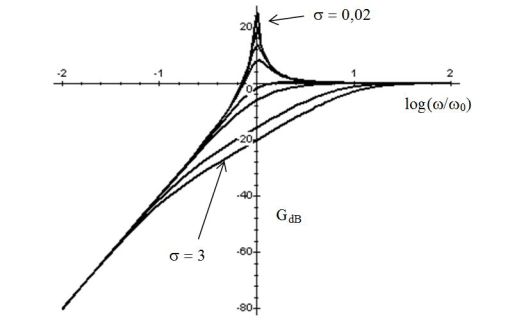
Les figures suivantes donnent le diagramme de Bode en gain et en phase d'un filtre passe-haut du 2nd ordre.
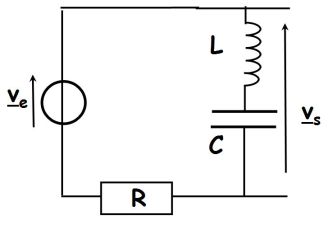
Fondamental : Aux bornes de (C + L) en sortie ouverte : filtre réjecteur ou coupe - bande
La règle du diviseur de tension donne :
\(\underline H (j\omega ) = \frac{{\frac{1}{{jC\omega }} + jL\omega \;}}{{R + jL\omega \; + \frac{1}{{jC\omega }}}} = \frac{{1 - LC{\omega ^2}}}{{1 - LC{\omega ^2} + jRC\omega \;}}\)
On souhaite écrire cette fonction de transfert sous la forme normalisée :
\(\underline H (j\omega ) = \frac{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}}}}{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}} + 2j\sigma \frac{\omega }{{{\omega _0}}}}}K\)
Par identification, on retrouve les mêmes caractéristiques :
\({\omega _0} = \frac{1}{{\sqrt {LC} }}\;\;\;\;\;;\;\;\;\;\;\sigma = \frac{1}{2}RC{\omega _0} = \frac{R}{2}\sqrt {\frac{C}{L}} \;\;\;\;\;;\;\;\;\;\;K = 1\)
Ainsi :
\(\underline H (j\omega ) = \frac{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}}}}{{1 - \frac{{{\omega ^2}}}{{\omega _0^2}} + 2j\sigma \frac{\omega }{{{\omega _0}}}}} = \frac{1}{{1 + \frac{{2j\sigma }}{{\left( {\frac{{{\omega _0}}}{\omega } - \frac{\omega }{\omega }} \right)}}}}\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;\left\{ \begin{array}{l}G(\omega ) = \frac{1}{{\sqrt {1 + \frac{{4{\sigma ^2}}}{{{{\left( {\frac{{{\omega _0}}}{\omega } - \frac{\omega }{\omega }} \right)}^2}}}} }} \\{\varphi _{rejecteur}} = {\varphi _{passe - bas}} \pm \pi \\\end{array} \right.\)
Les figures suivantes donnent le diagramme de Bode en gain et en phase d'un filtre réjecteur du 2nd ordre.