Light bulb ignition
Take 10 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
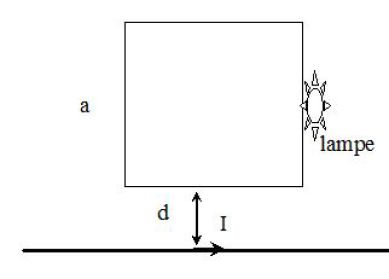
A plane coil of square-section of side \(a\) is put near a high voltage wire, travelled by the effective intensity \(I_{eff}\).
Its frequency is \(f\).
A light-bulb is added to one end of the coil and can only be turned on for a voltage \(E>E_{seuil}\).
Question
How many whorls are necessary for the light to turn on ?
Indice
Can you explain why the light can turn on ?
Think about Faraday's law.
Solution
The magnetic field created by the wire is : (Use Ampere's circuital law)
\(\vec B = \frac{{\mu _0 I(t)}}{{2\pi }}\frac{1}{r}\vec e_\theta= \frac{{\mu _0 I_{eff}\sqrt 2 \cos \omega t}}{{2\pi }}\frac{1}{r}\vec e_\theta\)
The flux of this field through the coil is :
\(\Phi = Na\int_d^{d + a} {B(r)dr} = \frac{{\mu _0 NaI_{eff}\sqrt 2 \cos \omega t}}{{2\pi }}\ln( \frac{{d + a}}{d})\)
Faraday's law gives the electromotive force that appears in the frame :
\(e = - \frac{{d\Phi }}{{dt}}=-\frac{{\mu _0 \omega NaI_{eff}\sqrt{2}}}{{2\pi }}\ln( \frac{{d + a}}{d})sin(\omega t)\)
The effective voltage at the edges of the light bulb is :
\(E = \frac{{\mu _0 \omega NaI_{eff}}}{{2\pi }}\ln (\frac{{d + a}}{d}) > E_{seuil}\)
Hence the minimum number of whorls in the coil can be deduced from the formula :
\(N>\frac{2\pi E_{seuil}}{\mu_0 \omega NaI_{eff}} \frac{1}{ln(\frac{d+a}{d})}\)