Mutual Inductance
Take 10 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
On a torus generated by the rotation of a circle of radius \(a\) are regularly wound \(N\) whorls travelled by a current \(i\).
On this winding \((P)\) is formed a coil \((C)\) made of \(n\) whorls of radius \(a\).
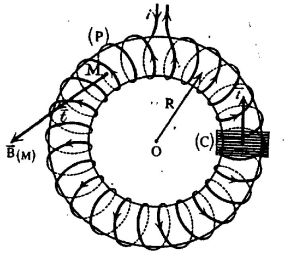
Question
Compute the coefficient of the mutual inductance \(M\) of the two windings \((P)\) and \((C)\).
Indice
How is \(M\) defined?
Which field is easier to compute ?
See the lesson about self inductance, mutual inductance where the magnetic field of the torus is calculated.
Solution
The flux of the magnetic field created by the torus on the coil is :
\(\phi = Mi\)
Where \(i\) is the current circulating through the torus.
Ampere's circuital law enables the determination of the field created by the torus inside. It is equal to zero outside.
\(\vec B = \frac{{\mu Ni}}{{2\pi }}\frac{1}{r}\vec u_\theta\)
To simplifiy the computation, the torus is supposed to be thin so that the magnetic field is uniform (\(r \approx R\)).
The flux through the coil becomes :
\(\phi = n\frac{{\mu Ni}}{{2\pi }}\frac{1}{R}\pi a^2\)
Hence :
\(M = \frac{{\mu _0 Nna^2 }}{{2R}}\)