Electromagnetic levitation
Take 20 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
A long, half infinite, vertical solenoid of circular section (of radius \(a\) and made of \(n\) joined whorls by length unit) is travelled by a current intensity :
\(i_1(t)=i_{1,m} cos \omega t\)
A circular coil made of \(N\) whorls of radius \(b<<a\), of résistance \(R\), inductance \(L\) and mass \(m\) is placed above the solenoid, distant from \(z\) to its end.
The position of the coil is marked by angle \(\theta\)
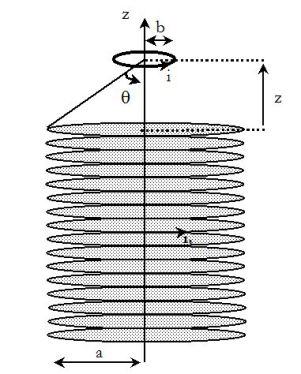
The magnetic field due to the solenoid at the center of the whorl is given by :
\(\vec B = \frac{{{\mu _0}n{i_{1,m}}\cos \omega t}}{2}(1 - \cos \theta ){\;\vec e_z}\)
With :
\(\tan \theta = \frac{a}{z}\)
Question
Determine the electric equation verified by the current \( i(t)\) induced in the coil.
We will write :
\(i(t)=I_mcos(\omega t+\varphi)\).
Indice
Calculate the mutual induction of the two circuits and use complex notation to solve the electrical equation.
Solution
Suppose the field is uniform at the surface of the whorl. Its flux through the coil is :
\(\Phi = \frac{{{\mu _0}nN\pi {b^2}}}{2}(1 - \cos \theta ){i_{1,m}}\cos \omega t\)
A mutual inductance between the whorl and the solenoid can be defined :
\(M = \frac{{{\mu _0}nN\pi {b^2}}}{2}(1 - \cos \theta )\;\;\;\;\;\;\;so\;\;\;\;\;\;\;\Phi = M{i_{1,m}}\cos \omega t\)
The electric equation of the coil is then :
\(Ri + L\frac{{di}}{{dt}} + M\frac{{d{i_1}}}{{dt}} = 0\)
In a forced sinusoidal state :
\(i = {I_m}{e^{j\omega t}}{e^{j\varphi }}\)
So :
\(Ri + jL\omega i + jM\omega {i_1} = 0\)
Hence :
\({I_m}{e^{j\varphi }} = - \frac{{jM\omega }}{{R + jL\omega }}{i_{1m}} = \frac{{M\omega }}{{jR - L\omega }}{i_{1m}}\)
It can be deduced :
\({I_m} = \frac{{M\omega }}{{\sqrt {{R^2} + {L^2}{\omega ^2}} }}{i_{1m}}\)
And :
\(\tan \varphi = \frac{R}{{L\omega }}\;\;\;\;(with\;\cos \varphi = - \frac{{L\omega }}{{\sqrt {{R^2} + {L^2}{\omega ^2}} }} < 0)\)
Question
Show that the radial magnetic field in the whorl can be written :
\(B_r(r,z)=-\frac{r}{2} \frac{dB_z(z,0)}{dz}\)
Indice
The magnetic field can be obtained by expressing the conservation of the magnetic flux.
Solution
Let's compute the radial component of the field.
Outside the \((Oz)\) axis, the magnetic field can be expressed :
\(\vec B(M)=B_r(r,z)\;\vec u_r+B_z (r,z) \;\vec u_z\)
We can notice that the plane défined by the point M and \((\vec u_r,\vec u_z)\) is a anti-symetrical plane for the current distribution along the wire, so the magnetic field is in this plane and has no coordinate along \(\vec u_{\theta}\).
Outside the axis, the magnetic field can be obtained by expressing the conservation of the magnetic flux :
\( \oint_S\vec {B}.\vec{n} \ dS=0\)
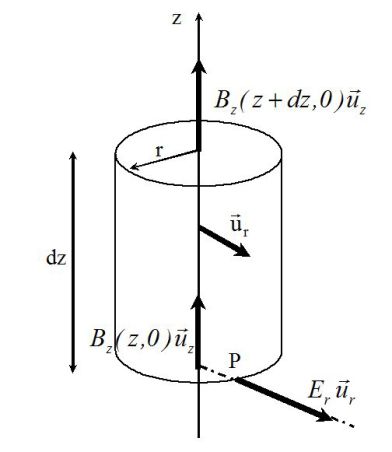
A small cylinder, centered on axis Oz, of height \(dz\) and small radius \(r\) is used.
The flux, exiting through this closed surface must be equal to zero :
\(\pi {r^2}B_z(z+dz,0)-\pi r^2B_z(z,0)+ 2\pi r dz{B_r}(r,z) = 0\)
Thus :
\(\pi {r^2}dB_z(z,0) + 2\pi r dz{B_r}(r,z) = 0\)
So :
\({B_r}(r,z) = - \frac{r}{2}\frac{{d{B_z}(z,0)}}{{dz}}\)
Question
Deduce the Laplace's force applied to the whorl.
Under which conditions is levitation possible ?
Is this possible equilibrium stable or unstable ?
Indice
Use the definition of the Laplace force and show that only the magnetic fied along \(\vec u_r\) is usefull.
Solution
The Laplace's force (mainly vertical) is :
\(d\vec f = id\ell {\vec u_\theta } \wedge {B_r (r,z)}{\vec u_r} = - i{B_r(r,z)}d\ell {\vec u_z}\)
So :
\(\vec F = i\pi N{b^2}\frac{{d{B_z}(z,0)}}{{dz}}{\vec u_z}\)
However :
\(\frac{{dB}}{{dz}} = \frac{{{\mu _0}n{i_{1,m}}\cos \omega t}}{2}\sin \theta \frac{{d\theta }}{{dz}}\)
And :
\(\frac{{d\theta }}{{dz}} = - \frac{1}{a}{\sin ^2}\theta\) (Use \(tan\theta=a/z\))
Thus :
\(\frac{{dB}}{{dz}} = - \frac{{{\mu _0}n{i_{1,m}}\cos \omega t}}{{2a}}{\sin ^3}\theta\)
The force becomes :
\(\vec F = - \frac{{\pi {b^2}{\mu _0}Nni{i_{1,m}}\cos \omega t}}{{2a}}{\sin ^3}\theta \;{\vec u_z}\)
Hence :
\(\vec F = - \frac{{\pi {b^2}{\mu _0}Nn{I_m}{i_{1,m}}\cos \omega t\cos (\omega t + \varphi )}}{{2a}}{\sin ^3}\theta \;{\vec u_z}\)
The mean value : (using \(\cos \omega t\cos (\omega t + \varphi ) = \frac{1}{2}(\cos (2\omega t + \varphi ) + \cos \varphi )\))
\(\left\langle {\vec F} \right\rangle = - \frac{{\pi {b^2}{\mu _0}nN{I_m}{i_{1,m}}}}{{4a}}{\sin ^3}\theta \;\cos (\varphi ){\vec u_z}\)
With :
\({I_m} = \frac{{M\omega }}{{\sqrt {{R^2} + {L^2}{\omega ^2}} }}{i_{1m}}\;\;\;and\;\;\;\cos \varphi = - \frac{{L\omega }}{{\sqrt {{R^2} + {L^2}{\omega ^2}} }}\)
It comes :
\(\left\langle {\vec F} \right\rangle = \frac{{\pi {b^2}{\mu _0}nNML{\omega ^2}i_{1m}^2}}{{4a({R^2} + {L^2}{\omega ^2})}}{\sin ^3}\theta \;{\vec u_z}\)
It is indeed a repulsive force (oriented upwards).
Right above the solenoid, \(\theta=\pi/2\).
Levitation is possible if the repulsion force is superior to the weight.
\(\frac{{\pi {b^2}{\mu _0}nNML{\omega ^2}i_{1m}^2}}{{4a({R^2} + {L^2}{\omega ^2})}} > mg\)
It is a stable equilibrium : if the mass goes up, the repulsion force diminishes and the mass goes back down.
Same if the mass begins by going down.
