A sound propagation model in the air
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
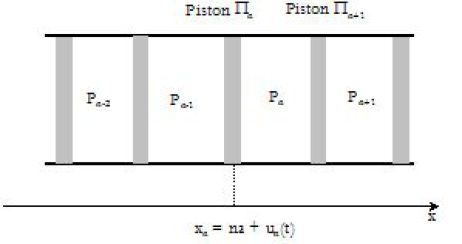
An insulated pipe of cross section \(S\) is divided into an infinite number of compartments (\(C_n\)) by insulated pistons \(P_n\) and \(P_{n+1}\) of cross section \(S\) and mass \(m\).
In each compartment is a mole of air, compared to a perfect gas evolving isentropically according to the law of Laplace, \(PV^\gamma = cste\).
At equilibrium, the abscissa of the piston (\(n\)) is :
\(x_{n,eq}=na\)
and pressure has the same value \(P_0\) in each compartment.
Besides the equilibrium position, the abscissa of the piston (\(n\)) is :
\(x_n(t)=na+u_n(t)\)
With \(\left| {u_n (t)} \right| < < a\) and the pressure in the compartment \((n)\) is \(P_n\).
Question
Establish the expression of the pressure \(P_n\) as the function of \(P_0\), \(g\), \(a\), \(u_n(t)\) and \(u_{n+1}(t)\) and the linearized using :
\(\left| {u_n (t)} \right| < < a\)
Deduce the linear differential equation determining the motion of the piston number (\(n\)).
Indice
Is Laplace checked ?
Do not forget that \(\left| {u_n (t)} \right| < < a\).
Solution
The application of the Laplace law for the gas in the compartment \(n\) leads to :
\({P_n} = {P_0}{(1 + ({u_{n + 1}(t)} - {u_n}(t))/a)^{ - \gamma }} \approx {P_0}(1 - \gamma ({u_{n + 1}(t)} - {u_n}(t))/a)\)
Question
The approximation of a continuous medium is done by defining a function \(u (x, t)\) varying little in the scale of \(a\), as \(u(na,t)=u_n(t)\).
Establish the partial differential equation whose solution is \(u (x, t)\).
Define a speed \(c\) and comment expression.
Solution
The Newton's second law applied to the piston number \(n\) gives:
\({\ddot u_n(t)} = (\gamma S{P_0}/ma)({u_{n + 1}(t)} + {u_{n - 1}(t)} - 2{u_n}(t))\)
The approximation of continuous medium resulting in :
\(\begin{array}{l}{u_{n + 1}}(t) = u((n + 1)a,t) = u(na,t) + \frac{{\partial u(na,t)}}{{\partial t}}a + \frac{1}{2}\frac{{{\partial ^2}u(na,t)}}{{\partial {t^2}}}{a^2} \\{u_{n - 1}}(t) = u((n - 1)a,t) = u(na,t) - \frac{{\partial u(na,t)}}{{\partial t}}a + \frac{1}{2}\frac{{{\partial ^2}u(na,t)}}{{\partial {t^2}}}{a^2} \\\end{array}\)
Whence :
\(\frac{{{\partial ^2}u(x,t)}}{{\partial {x^2}}} - \frac{1}{{{c^2}}}\frac{{{\partial ^2}u(x,t)}}{{\partial {t^2}}} = 0\)
With :
\(c = \sqrt {\frac{{\gamma {P_0}Sa}}{m}}\)
\(c\) increases if the environment is more rigid (\(P_0\) increases) and less inert (\(m\) decreases), which is natural for mechanical waves.
Question
Evaluate the speed \(c\) of sound in air assuming that the piston mass \(m\) of the model are in fact constituted by the volume of air \(V = Sa\) between two pistons in the model.
We give :
\(\gamma = 1,4\;;\;P_0 = 1\;bar\;;\;\mu _0 = 1,3\;kg.m^{ - 3}\)
Solution
We find : \(c=328\;m.s^{-1}\) (in good agreement with the expected value)