Transversal oscillations of a leaded rope
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
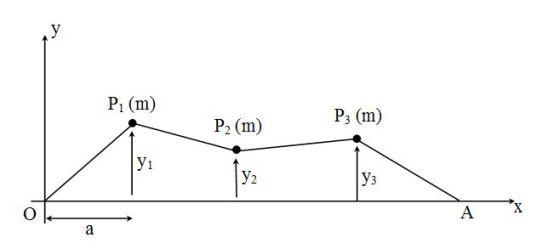
An elastic cord of negligible mass is at equilibrium, tense with a force \(F\) between two fixed points \(O\) and \(A\) of a distance \(4a\) from each other.
The rope supports, regularly spaced, three weights \(P_1\), \(P_2\) and \(P_3\) of the same mass \(m\).
Neglecting the weight of the leads, each string section of length is \(a\) in the initial equilibrium state is characterized by the stiffness of the string \(k\) and natural length \(\ell_0<a\).
Let \(\omega_0^2=F/ma\).
Small transverse movements of the leads are studied ; ordinate of lead \(P_n\) is \(y_n(t)\) at time \(t\) (\(\left| {y_n(t)} \right|<<a\)).
It is assumed that its abscissa is constantly equal to \(x_n = na\).
Question
Establish a differential system of the second order relative to the studied movement.
Indice
Apply the Newton's second law to each lead.
Remember, the amplitudes are low.
Solution
The Newton's second law applied to each lead in vertical projection gives :
\(\begin{array}{l}m\ddot y_1(t) = - F\frac{{y_1 (t)}}{a} - F\frac{{y_1(t) - y_2(t) }}{a} \\m\ddot y_2(t) = F\frac{{y_1(t) - y_2(t) }}{a} - F\frac{{y_2(t) - y_3(t) }}{a} \\m\ddot y_3 (t)= - F\frac{{y_3(t) - y_2(t) }}{a} - F\frac{{y_3 }(t)}{a} \\\end{array}\)
So :
\(\begin{array}{l}\ddot y_1(t) = \omega _0^2 ( - 2y_1(t) + y_2(t) ) \\\ddot y_2(t) = \omega _0^2 (y_1(t) - 2y_2(t) + y_3(t) ) \\\ddot y_3(t) = \omega _0^2 (y_2(t) - 2y_3(t) ) \\\end{array}\)
Question
We seek the solution of type \(y_n=a_ncos\omega t\) (all weights vibrating in phase with the same frequency).
Determine the possible values of \(\omega\) for such movements (proper modes of the system).
Solution
The linear system is obtained :
\(\begin{array}{l}(\omega ^2 - 2\omega _0^2 )\;a_1 + \omega _0^2 \;a_2 = 0 \\\omega _0^2\; a_1 + (\omega ^2 - 2\omega _0^2 )\;a_2 + \omega _0^2\; a_3 = 0 \\\omega _0^2 \;a_2 + (\omega ^2 - 2\omega _0^2 )\;a_3 = 0 \\\end{array}\)
This system has nontrivial solutions if the determinant is zero :
\(\left| \begin{array}{l}\omega ^2 - 2\omega _0^2 \;\;\;\;\;\;\;\;\;\omega _0^2 \;\;\;\;\;\;\;\;\;\;\;\;0 \\\;\;\;\;\;\omega _0^2 \;\;\;\;\;\;\;\;\omega ^2 - 2\omega _0^2 \;\;\;\;\;\;\;\omega _0^2 \;\; \\\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;\;\omega _0^2 \;\;\;\;\;\;\;\;\omega ^2 - 2\omega _0^2 \\\end{array} \right|\; = \;0\)
We then obtain three angular frequencies of the oscillations :
\(\omega _1 = \omega _0 \sqrt {2 - \sqrt 2 } \;\;\;\;\;;\;\;\;\;\;\omega _2 = \omega _0 \sqrt 2 \;\;\;\;\;;\;\;\;\;\;\omega _3 = \omega _0 \sqrt {2 + \sqrt 2 }\)
Simulation : Amazing pendulum wave effect
Do you know how to build this wave pendulum ?