Waves in a pool
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
Consider a perfect incompressible fluid (density \(\rho\)) in a basin of width \(L\) (along Oy).
A wave propagates along (Ox). The velocity field is of the form :
\(\vec v=v_x(x,z,t)\;\vec u_x+v_z(x,z,t)\;\vec u_z\)
The pressure \(P(x,z,t)\) is hydrostatic in the canal.
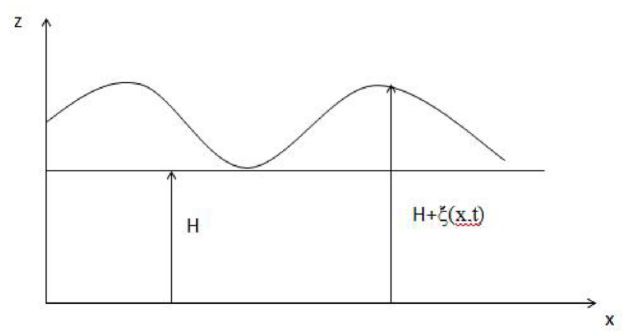
Note \(H+\xi (x,t)\) the height of the water in the canal (\(H\) is a constant).
The flow is assumed irrotational.
Question
Applying the Euler equation to a fluid particle, find a differential equation between \(v_x\) and \(\xi\) assuming small movements.
Show that \(v_x\) is indépendent of \(z\).
Solution
The Euler equation is :
\(\rho \left( {\frac{{\partial \vec v}}{{\partial t}} + (\vec v.\overrightarrow {grad} )\vec v} \right) = - \overrightarrow {grad} P + \rho \vec g\)
The pressure is hydrostatic, which means it is given by the expression obtained in fluid statics, namely :
\(P(x,z,t) = {P_0} + \rho g(H + \xi (x,t) - z)\)
Assuming small movements, it keeps only the first order terms (similar approximation to the acoustic approximation for the study of waves in fluids).
The Euler equation becomes :
\(\rho \frac{{\partial \vec v}}{{\partial t}} = - \overrightarrow {grad} P + \rho \vec g\)
In projection along the horizontal, the differential equation is obtained between \(v_x\) and \(\xi\) :
\(\rho \frac{{\partial {v_x}}}{{\partial t}} = - \frac{{\partial P}}{{\partial x}} = - \rho g\frac{{\partial \xi }}{{\partial x}}\)
Is :
\( \frac{{\partial {v_x}}}{{\partial t}} = - g\frac{{\partial \xi }}{{\partial x}}\)
The flow is incompressible, so :
\(div(\vec v) = \frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_z}}}{{\partial z}} = 0\)
In order of magnitude, if we note \(\lambda\) the wavelength of the wave (in the direction (Ox)) and \(a\) a characteristic dimension of the vertical movement (with \(a<<\lambda\)) :
\(\frac{{\left| {{v_x}} \right|}}{\lambda } \approx \frac{{\left| {{v_z}} \right|}}{a}\;\;\;\;so\;\;\;\;\;\left| {{v_z}} \right| \approx \frac{a}{\lambda }\left| {{v_x}} \right| < < \left| {{v_x}} \right|\)
We can therefore neglect the vertical component of velocity.
The flow is irrotational :
\(\overrightarrow {rot}( \vec v) = \vec 0\)
This leads to, neglecting \(v_z\) :
\(\frac{{\partial {v_x}}}{{\partial z}} = 0\)
Therefore, \(v_x\) does not depend on \(z\).
Question
Compute the volume flow rate \(Q_v\).
Make a mass balance on a slice of thickness \(dx\).
Deduce a differential equation between \(v_x\) and \(\xi\) assuming small movements.
Solution
The volume flow rate is :
\({Q_v}(x,t) = {v_x}(x,t)L(H + \xi (x,t))\)
Mass balance on a slice of thickness \(dx\), located between \(x\) and \(x+dx\) :
\(dm\) is the mass variation in this slice. It can be written in two ways :
\(dm = \rho L(H + \xi (x,t + dt))dx - \rho L(H + \xi (x,t))dx = \rho L\frac{{\partial \xi (x,t)}}{{\partial t}}dxdt\)
Or :
\(dm = \rho {Q_v}(x,t)dt - \rho {Q_v}(x + dx,t)dt = - \rho \frac{{\partial {Q_v}}}{{\partial x}}dxdt = - \rho L\frac{\partial }{{\partial x}}\left( {{v_x}(x,t)(H + \xi (x,t))} \right)dxdt\)
For identification :
\(\frac{{\partial \xi (x,t)}}{{\partial t}} = - \frac{\partial }{{\partial x}}\left( {{v_x}(x,t)(H + \xi (x,t))} \right)\)
The first order :
\(\frac{{\partial \xi (x,t)}}{{\partial t}} = - H\frac{{\partial {v_x}(x,t)}}{{\partial x}}\)
Question
Show that \(v_x\) and \(\xi\) check each classical wave equation.
Deduce the velocity of propagation of waves in the channel.
Solution
It was also the two equations :
\(\frac{{\partial \xi (x,t)}}{{\partial t}} = - H\frac{{\partial {v_x}(x,t)}}{{\partial t}}\)
And :
\( \frac{{\partial {v_x}(x,t)}}{{\partial t}} = - g\frac{{\partial \xi(x,t) }}{{\partial x}}\)
By decoupling these two equations, we arrive at the d'Alembert equation :
\(\frac{{{\partial ^2}\xi (x,t)}}{{\partial {x^2}}} - \frac{1}{{{c^2}}}\frac{{{\partial ^2}\xi (x,t)}}{{\partial {t^2}}} = 0\;\;\;\;\;and\;\;\;\;\;\frac{{{\partial ^2}{v_x}(x,t)}}{{\partial {x^2}}} - \frac{1}{{{c^2}}}\frac{{{\partial ^2}{v_x}(x,t)}}{{\partial {t^2}}} = 0\)
Where the wave propagation speed is :
\(c=\sqrt{gL}\)