Sound propagation in solids
Fondamental : Infinite chain of oscillators and approximation of continuous medium
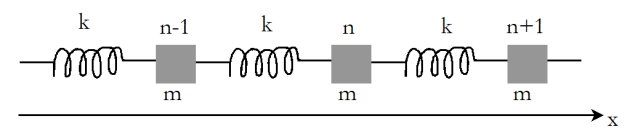
To study the propagation of sound waves in solids, the following model is used (see figure) :
The solid consists of an endless chain of punctual atoms, mass \(m\), interconnected by springs of spring constant \(k\) and their original length \(a\) (corresponding to the inter-atom distance at equilibrium).
The elastically coupled atom chain (linear restoring) by springs is a simple model to describe the spread of small vibratory motions in a solid, that is to say, the propagation of sound in a solid.
The latter is in fact composed of regular stacks of atoms (ions or molecules).
Forces restoring an atom to its equilibrium position may be modeled, in the linear term, by elastic restoring, to the extent that the amplitudes of vibration of the atoms are low (it is assumed here that the solid is homogeneous and isotropic).
The movement of the ensemble occurs without friction along the axis (Ox).
Atoms move slightly about their respective equilibrium positions, which can identify the form \(x_{eq,n}=na\).
We reference the positions of the atoms out of equilibrium by their abscissa :
\(x_n(t)=na+u_n(t)\)
Where the displacement \(u_n(t)\) remains low with respect to \(a\).
The second Newton's law applied to the \((n)\) rank atom provides, in projection :
\(m\ddot x_n(t) = - k(u_n(t) - u_{n - 1}(t) ) + k(u_{n + 1}(t) - u_n(t) ) = - k(2u_n(t) - u_{n - 1}(t) - u_{n + 1}(t) )\)
The distance inter-atom is of the order of \(a\approx 10^{-10}\;m\), distance much smaller than the characteristic distances of the propagation phenomena that is being studied, in particular the wavelength of vibration (of the order of \(25\; cm\) at \(20\; kHz\)). Therefore, \(u_n(t)\) changes very little over the distance \(a\).
It will thereby define a continuous function of \(u\) as follows : (approximation of continuous medium)
\(u(x_{eq,n},t)=u_n(t)\)
It comes then (Taylor-Young expansion of the second order) :
\(\left\{ \begin{array}{l}u_{n + 1} (t) = u(x_{eq,n + 1} ,t) = u(x_{eq,n} + a,t) = u(x_{eq,n} ,t) + \frac{{\partial u}}{{\partial x}}a + \frac{1}{2}\frac{{\partial ^2 u}}{{\partial x^2 }}a^2 \\u_{n - 1} (t) = u(x_{eq,n - 1} ,t) = u(x_{eq,n} - a,t) = u(x_{eq,n} ,t) - \frac{{\partial u}}{{\partial x}}a + \frac{1}{2}\frac{{\partial ^2 u}}{{\partial x^2 }}a^2 \\\end{array} \right.\)
And the equation of motion becomes :
\(m\frac{{\partial ^2 u(x,t)}}{{\partial t^2 }} = k\left( {\frac{{\partial ^2 u(x,t)}}{{\partial x^2 }}\;a^2 } \right)\)
And :
\(\frac{{\partial ^2 u(x,t)}}{{\partial x^2 }} - \frac{1}{{c^2 }}\frac{{\partial ^2 u(x,t)}}{{\partial t^2 }} = 0\;\;\;\;\;\;\;\;\;\;with\;\;\;\;\;\;\;\;\;\;c = \sqrt {\frac{{ka^2 }}{m}}\)
This is the d'Alembert wave equation, already obtained in the chapter on "Electromagnetic waves in vacuum".
We know that it is associated with a wave phenomenon of celerity \(c\).
This speed should not be confused with the speed of longitudinal movement of the atoms \(\frac {\partial u(x,t)}{\partial t}\).
The waves are longitudinal here because the movement of atoms is in the direction of propagation.
Complément :
The following video, proposed by Yves Pelletier :
Acoustics and vibration animations (by Daniel A.Russell) : click here
Mechanical waves are waves which propagate through a material medium (solid, liquid, or gas) at a wave speed which depends on the elastic and inertial properties of that medium.
There are two basic types of wave motion for mechanical waves : longitudinal waves and transverse waves.
The animations demonstrate both types of wave and illustrate the difference between the motion of the wave and the motion of the particles in the medium through which the wave is travelling.
Fondamental : Relationship to Young's modulus
Phenomenological Hooke's law :
Needed \(dF(x,t)\) force perpendicular to a surface \(dS\) of a solid to cause a displacement \(u (x, t)\) is :
\(dF(x,t) = Y\frac{{\partial u(x,t)}}{{\partial x}}dS\)
Where \(Y\) denotes Young's modulus.
\(Y\) can be expressed in terms of microscopic quantities defined above (\(k\), \(m\) and \(a\)).
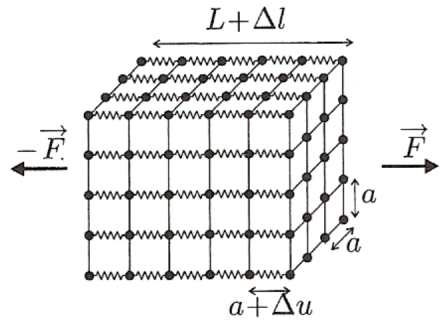
For this, consider a three-dimensional solid model consisting of chains of atoms associated in parallel such that at equilibrium the atoms are located at the summits of a cubic lattice nearest distance between lattice points \(a\) and axis (Ox), (Oy) and (Oz).
In such a network, each cube has side contains \(8\) atoms placed on its \(8\) summits, each atom being common to \(8\) cubes that touch at this point.
It is therefore \(8/8=1\) atom of mass \(m\) per cub of volume \(a^3\), which allows to express the density of the solid :
\(\mu=\frac {m}{a^3}\)
We consider a deformation of the solid along (Ox) as the atoms located in \(na\) at equilibrium are in \(x_n(t)=na+u_n(t)\) in the presence of the deformation.
\(dS\) is a surface of this solid cut in the \(x_n-axis\) plane.
The force exerted by the atom \(n+1\) of a string on the atom \(n\) is :
\(f = k(x_{n + 1}(t) - x_n(t) - a)\)
The surface \(dS\) contains \(dS/a^2\) chains of atoms playing the same role.
So the force exerted by the part of the right side of \(dS\) on the part of the left side of \(dS\) is :
\(dF = \left( {\frac{{dS}}{{a^2 }}} \right)k(x_{n + 1}(t) - x_n(t) - a) = \frac{k}{{a^2 }}(u_{n + 1}(t) - u_n(t) )dS\)
In the approximation of continuous medium :
\(dF (x,t)= \frac{k}{{a^2 }}\left( {\frac{{\partial u(x,t)}}{{\partial x}}a} \right)dS = \frac{k}{a}\frac{{\partial u(x,t)}}{{\partial x}}\;dS\)
It is thus demonstrated Hooke's law, with the Young's modulus :
\(Y=\frac {k}{a}\)
It is noted that \(Y\) is equivalent to a force by a surface or a pressure.
The sound propagation speed in the solid can be expressed in terms of \(Y\) :
Relations :
\(c = \sqrt {\frac{{ka^2 }}{m}} \;\;\;\;\;;\;\;\;\;\;\mu = \frac{m}{{a^3 }}\;\;\;\;\;;\;\;\;\;\;Y = \frac{k}{a}\)
finally give :
\(c = \sqrt {\frac{Y}{\mu }}\)
Fondamental : Mesoscopic study
One can get the d'Alembert equation by direct mesoscopic study of elastic material studied.
For this, we take a slice of material of thickness \(dx\), surface \(dS\) and therefore mass \(\mu dS dx\).
It undergoes, according to Hooke's Law, a force \(dF(x +dx,t)\) at \(x + dx\) and by action and reaction, a force \(– dF(x,t)\) at \(x\) (the differential element for forces is not related to the elementary thickness \(dx\), but the elementary surface \(dS\)).
The Newton's second law provides :
\(\mu dSdx\;\frac{{\partial ^2 u(x,t)}}{{\partial t^2 }} = dF(x + dx,t) - dF(x,t) = \frac{{\partial (dF(x,t))}}{{\partial x}}dx = YdS\frac{{\partial ^2 u(x,t)}}{{\partial x^2 }}dx\)
Where the wave equation :
\(\frac{{\partial ^2 u(x,t)}}{{\partial t^2 }} - \frac{1}{{c^2 }}\frac{{\partial ^2 u(x,t)}}{{\partial x^2 }} = 0\;\;\;\;\;with\;\;\;\;\;c= \sqrt {\frac{Y}{\mu }}\)
Numerical applications :
For \(Y=10^{11}\;N.m^{-2}\) and \(\mu = 3\) at \(10.10^3\;kg.m^{-3}\), was \(c\approx 3\;000\) at \(5\;000\;m.s^{-1}\), the rank of velocity magnitude of acoustic waves of waves in a solid.