Take 5 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
Prove that the familly
is a linearly independent familly of the vector space of the applications from
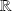to
Consider a linear combination of the two functions, then take two well chosen values for the variable.
Let us consider a zero linear combination of these two vectors,
We denoted by
here the zero vector of the vector space of the applications from
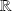to
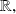meaning the zero application.
We have the equality of two applications from
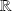to
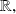meaning that they have the same value in any point of
We therefore have:
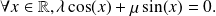
By giving
the value
we obtain
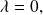then by giving
the value
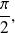we obtain
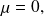which implies that the family is linearly independent.
