Take 10 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
We denote by
and
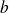two relative integers and by
the polynomial defined by
Prove that polynomial
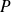takes an integer value in
as well as all its derivative polynomials.
Develop
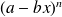with the binomial formula, then apply Taylor's formula to polynomial
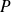(by noticing that the derivatives of an d'order strictly greater than
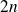of the polynomial are zero) and identify the two expressions.
We notice that
is a root of order
of polynomial
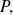therefore
is a root of
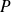and of the derivative polynomials
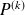for any natural integer
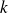lower or equal to
We then apply Taylor's formula, noticing that polynomial has a degree of
hence its derivatives of order strictly greater than
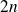are zero.
We get:
Using the binomial formule, we also have:
Therefore we have:
In the left member, we make the index substitution
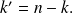We obtain:
which gives us, simplifying by
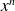and going back to index
since the index name does not matter:
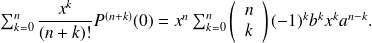
Identifying the coefficients of identical degrees of both polynomials, we infer:
and finally:
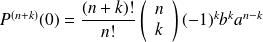which is a relative integer.
