Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
Calculate
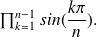
Express
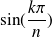with Euler's formula then factorize by
in the term
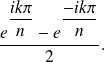
The desired product can then by divided in two products. One of them is calculated with usual properties of the exponential application, the other one can be interpreted as the limit when
goes towards
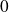of
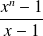(by factorizing polynomial
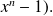
By Euler's formula,
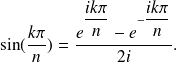
We set
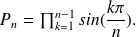
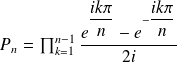
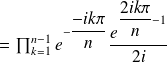
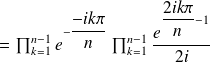
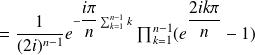
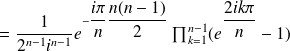
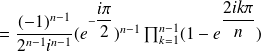
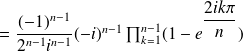
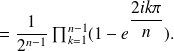
Let us consider now polynomial
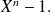
The roots of this polynomial are the
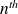roots of
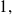hence the complex numbers
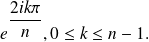
The Gauss's factorization of the polynomial gives us:
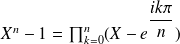therefore, for any real number
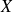different from
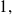we have:
We then go to the limit when
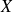goes towards
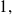the right member goes towards
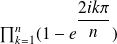and the left member goes towards the derivative value in
of function
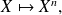meaning
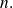
We conclude that
