Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
We denote by
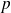 a non zero natural integer and we define an application
a non zero natural integer and we define an application
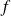 from
from
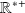 to
to
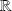 by:
by:
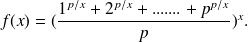
Find
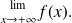
Set
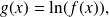 then make a Taylor-expansion of order
then make a Taylor-expansion of order
 of
of
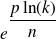 and get back to a form
and get back to a form
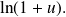
Application
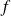 has strictly positive values, hence we can set
has strictly positive values, hence we can set
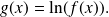
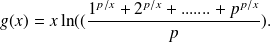
For any natural integer
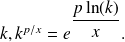
Since
 goes towards
goes towards
 when
when
 goes to
goes to
 we can use a Taylor-expansion of the exponential application, and we obtain:
we can use a Taylor-expansion of the exponential application, and we obtain:

We infer:
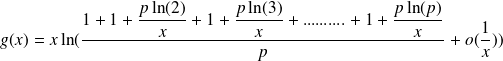
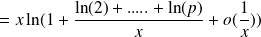
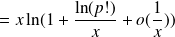
Since
 goes towards
goes towards
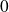 when
when
 goes to
goes to
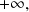 we obtain by using a Taylor-expansion of
we obtain by using a Taylor-expansion of
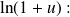
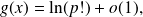 therefore:
therefore:
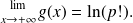
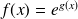 and the exponential application is continuous, therefore:
and the exponential application is continuous, therefore: