Take 10 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
We denote by
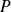 a polynomial.
a polynomial.
Prove that equation
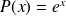 has only a finite number of roots.
has only a finite number of roots.
Apply successively several times Rolle's theorem, until the polynomial disappears.
Let
 be the degree of the polynomial. We set
be the degree of the polynomial. We set
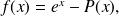 the number of roots of equation
the number of roots of equation
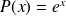 is equal to the number of zeros of application
is equal to the number of zeros of application
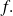
Let us assume that application
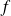 has
has
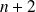 zeros, from the result of the previous exercise, this implies that application
zeros, from the result of the previous exercise, this implies that application
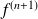 takes the zero value at least once.
takes the zero value at least once.
However the derivative of order
 of a polynomial of degree
of a polynomial of degree
 is zero, hence
is zero, hence
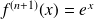 which is never zero.
which is never zero.
The equation has therefore at most
 solutions.
solutions.





