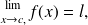Take 5 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
Prove that if an application
defined on an open interval
except in point
is such that:
then
has a limit when
goes towards
equal to
Write the definitions of right-sided and left-sided limits when
goes towards
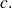
We obtain two strictly positive real numbers
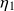and
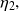set
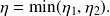
Let
be a strictly positive real number.
We have
hence:
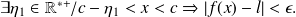
We also have
hence :
We set
and we obtain:
is equivalent to
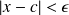and we can have this reasonning for any strictly positive real number
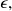hence we proved
