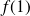Take 10 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel to ask then on the forum.
Question
Let
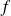 be a differentiable application from
be a differentiable application from
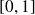 to
to
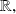 such that
such that
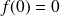 and
and
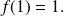
Let
 be a non zero natural integer, prove that there exists
be a non zero natural integer, prove that there exists
 real numbers
real numbers
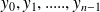 belonging to
belonging to
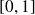 such that
such that
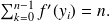
Slice the segment
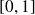 in
in
 segments of equal length and apply the Rolle's theorem to each of them.
segments of equal length and apply the Rolle's theorem to each of them.
Let us consider the steady subdivision of step
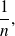 meaning:
meaning:
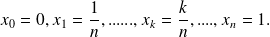
From the formula of mean values:
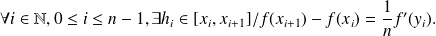
By summing the previous equalities for
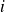 from
from
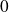 to
to
 we obtain:
we obtain:
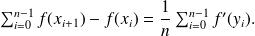
The terms of the sum of the left member of the previous equality are zero when taken two by two, meaning there remains
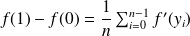 which gives us the expected result using the hypotheses on
which gives us the expected result using the hypotheses on
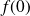 and
and