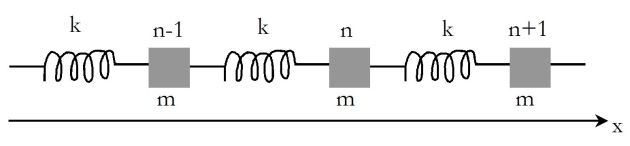
Dispersion sur une chaîne d'atomes
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On veut montrer qu'il existe des ondes élastiques longitudinales de pulsation \(\omega\) et de vecteur d'onde \(\vec k = k \vec u_x\) pouvant se propager le long d'un e chaîne infinie d'atomes, de masse m, de constante de raideur K et de positions au repos \(x_0^n=na\).
En notation complexe, le déplacement de la masse numérotée n est :
\(\underline u_n = Ae^{i(\omega t - kx_0^n)}\)
Question
Pourquoi A ne dépend-il pas de n ?
Solution
L'onde n'est ni stationnaire ni amortie : tous les atomes ont donc même amplitude pour une onde progressive. Le système est globalement invariant par translation.
Ainsi, A ne dépend pas de l'atome considéré.
Question
Déterminer, en fonction de \(k\), les valeurs possibles de la pulsation \(\omega\) des ondes susceptibles de se propager sur la chaîne.
Que déduit-on de la non linéarité de cette relation ?
Solution
Le PFD appliqué à l'atome numéroté n donne :
\(m{\ddot u_n} = - K({u_n} - {u_{n - 1}}) + K({u_{n + 1}} - {u_n}) = - K(2{u_n} - {u_{n - 1}} - {u_{n + 1}})\)
On injecte la solution proposée dans cette équation :
\(-m\omega ^2=K(e^{ika}+e^{-ika}-2)=-2K(1-coska)\)
Soit :
\(\omega (k) = 2\sqrt {\frac{K}{m}} \left| {\sin \left( {\frac{{ka}}{2}} \right)} \right|\)
Cette relation de dispersion est non linéaire : il y a dispersion.
Question
Calculer les vitesses de phase \(v_{\varphi}(k)\) et de groupe \(v_g(k)\).
Donner leurs limites pour \(ka\to 0\) et \(ka \to \pi\) et les commenter.
Solution
La vitesse de phase est : (on se place dans la suite dans le cas où \(0<ka<\pi\))
\({v_\varphi } = \frac{\omega }{k} = 2\sqrt {\frac{K}{m}} \frac{{\sin \left( {\frac{{ka}}{2}} \right)}}{k}\)
Et la vitesse de groupe :
\({v_g} = \frac{{d\omega }}{{dk}} = a\sqrt {\frac{K}{m}} \cos \left( {\frac{{ka}}{2}} \right)\)
Pour \(ka \to 0\) (donc des grandes longueurs d'onde) :
\({v_\varphi } \approx {v_g} = a\sqrt {\frac{K}{m}}\)
On retrouve les vitesses obtenues dans l'approximation des milieux continus.
Et pour \(ka \to \pi\) :
\({v_\varphi } \approx \frac{{2a}}{\pi }\sqrt {\frac{K}{m}}\)
Et :
\(v_g \approx 0\)
L'onde ne passe plus.