Équation de propagation de Klein-Gordon
Consacrer 10 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
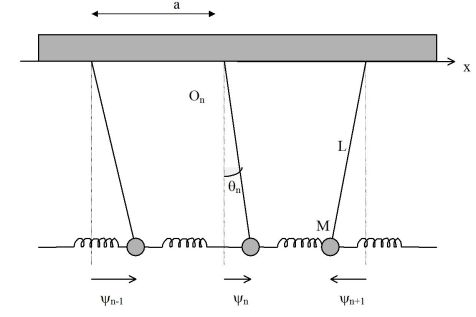
On étudie la propagation d'onde le long d'une chaîne de pendules simples, identiques, de masse M et de longueur L, couplés par des ressorts de constante K, représentés sur la figure ci-dessous :
On notera :
\(\omega _0 = \sqrt {K/M}\) et \( \Omega _0 = \sqrt {g/L}\)
Question
Quelle est l'équation de propagation liant les petits déplacements \(\psi _n \approx L\theta _n\), \(\psi _{n-1}\) et \(\psi _{n+1}\) des extrémités des pendules ?
Indice
Utiliser le théorème du moment cinétique pour chaque pendule par rapport au point d'attache \(O_n\).
Solution
Le théorème du moment cinétique appliqué au pendule (n) donne :
\(M{L^2}{\ddot \theta _n} = - MgL{\theta _n} + KL({\theta _{n - 1}} - 2{\theta _n} + {\theta _{n + 1}})\)
D'où l'équation de propagation :
\({\ddot \theta _n} = - \Omega _0^2{\theta _n} + \omega _0^2({\theta _{n - 1}} - 2{\theta _n} + {\theta _{n + 1}})\)
Question
Quelle est la relation de dispersion des ondes progressives monochromatiques caractérisant cette propagation ?
Indice
Il faut chercher des solutions de l'équation de propagation sous forme d'ondes planes.
Solution
On cherche des solutions sous la forme d'ondes planes :
\({\underline \theta }_n = A{e^{i(\omega t - kx)}}\)
Ainsi :
\(- {\omega ^2}{A^{i(\omega t - nka)}} = - \Omega _0^2{A^{i(\omega t - nka)}} + \omega _0^2({A^{i(\omega t - (n - 1)ka)}} - 2{A^{i(\omega t - nka)}} + {A^{i(\omega t - (n + 1)ka)}})\)
Soit :
\(- {\omega ^2} = - \Omega _0^2 + \omega _0^2{(^{ika}} - 2 + {A^{ - ika)}}) = - \Omega _0^2 + \omega _0^2(2\cos ka - 2)\)
Finalement :
\({\omega ^2} = \Omega _0^2 + 4\omega _0^2{\sin ^2}\left( {\frac{{ka}}{2}} \right)\)
Question
Représenter la relation de dispersion en précisant la bande permise pour les pulsations d'oscillations libres de la chaîne de pendules couplés.
Solution
L'intervalle de pulsations possible est (zone de Brillouin) : \(\left[ {\Omega _0^{},\sqrt {\Omega _0^2 + 4\omega _0^2} } \right]\)
On peut tracer ω en fonction de k (figure ci - dessous).

Question
Préciser la forme prise par ces résultats dans l'approximation des milieux continus.
Solution
Dans l'approximation des milieux continus :
\({\theta _n}(t) = \theta (na,t)\)
Alors :
\({\theta _{n - 1}}(t) = \theta ((n - 1)a,t) = \theta (na,t) - \frac{{\partial \theta (na,t)}}{{\partial x}}a + \frac{1}{2}\frac{{{\partial ^2}\theta (na,t)}}{{\partial {x^2}}}{a^2}\)
\({\theta _{n - 1}}(t) = \theta ((n - 1)a,t) = \theta (na,t) - \frac{{\partial \theta (na,t)}}{{\partial x}}a + \frac{1}{2}\frac{{{\partial ^2}\theta (na,t)}}{{\partial {x^2}}}{a^2}\)
En reportant dans l'équation de propagation :
\(\frac{{{\partial ^2}\theta }}{{\partial {t^2}}} = - \Omega _0^2\theta + \omega _0^2\frac{{{\partial ^2}\theta }}{{\partial {x^2}}}{a^2}\)
Finalement :
\(\frac{{{\partial ^2}\theta }}{{\partial {t^2}}} - {c^2}\frac{{{\partial ^2}\theta }}{{\partial {x^2}}} + \Omega _0^2\theta = 0\)
C'est l'équation de Klein-Gordon.
La relation de dispersion prend alors la forme :
\(- {\omega ^2}\theta - {c^2}( - {k^2}\theta ) + \Omega _0^2\theta = 0\;\;\;\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;\;\;\;{k^2} = \frac{{{\omega ^2} - \Omega _0^2}}{{{c^2}}}\)