Relation de Bernoulli
Fondamental : Cas d'un écoulement parfait, stationnaire, irrotationnel, incompressible et homogène
La démonstration proposée dans cette fiche de cours est basée sur l'intégration de l'équation d'Euler.
C'est une méthode plus technique que celle présentée dans la vidéo "La physique animée".
On suppose dans la suite que la seule force volumique (autre que les forces de pression) est le poids.
L'équation d'Euler devient :

En notant : (l'axe (Oz) est orienté vers le haut)

Alors :

D'où :

Un champ scalaire dont le gradient est nul est indépendant du point M ; c'est une fonction du temps uniquement f(t).
Comme l'écoulement est stationnaire, cette fonction est constante :

C'est le théorème de Bernoulli, qui affirme que la quantité
 reste en tout point du fluide égale à une même constante.
reste en tout point du fluide égale à une même constante.
Remarque :
On remarque que
 et
et
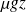 désignent les énergies volumiques cinétique et potentielle (de pesanteur), homogènes à une pression.
désignent les énergies volumiques cinétique et potentielle (de pesanteur), homogènes à une pression.
Remarque :
Dans le cas particulier où
 , on retrouve la relation fondamentale de l'hydrostatique des fluides :
, on retrouve la relation fondamentale de l'hydrostatique des fluides :

Attention : Relation de Bernoulli pour un écoulement parfait, stationnaire, irrotationnel, incompressible et homogène

La constante est la même pour tous les points du fluide.
Fondamental : Cas d'un écoulement parfait, stationnaire, incompressible et homogène
On renonce à l'hypothèse « écoulement irrotationnel ». Alors :


Afin d'éliminer le terme en rotationnel, on multiplie scalairement par
 et on intègre le long d'une ligne de courant entre deux points A et B :
et on intègre le long d'une ligne de courant entre deux points A et B :

En tout point,
 est parallèle au champ des vitesses : le terme
est parallèle au champ des vitesses : le terme
 est donc nul.
est donc nul.
Ainsi :

Soit :

Ainsi, l'abandon de l'hypothèse « écoulement irrotationnel » restreint le théorème de Bernoulli aux points A et B d'une même ligne de courant.
Attention : Relation de Bernoulli pour un écoulement parfait, stationnaire, incompressible et homogène
L'abandon de l'hypothèse « écoulement irrotationnel » restreint le théorème de Bernoulli aux points A et B d'une même ligne de courant :

Fondamental : Cas d'un écoulement parfait, non stationnaire, irrotationnel, incompressible et homogène
L'équation d'Euler devient :

Soit :

Comme
 , on peut définir un potentiel des vitesses tel que :
, on peut définir un potentiel des vitesses tel que :

Alors, avec :

Il vient :
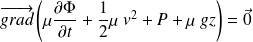
Soit une généralisation du théorème de Bernoulli dans le cas non stationnaire :

Où
 est une fonction du temps uniquement.
est une fonction du temps uniquement.
Attention : Relation de Bernoulli pour un écoulement parfait, non stationnaire, irrotationnel, incompressible et homogène

Où
 est une fonction du temps uniquement et
est une fonction du temps uniquement et
 est le potentiel des vitesses défini par :
est le potentiel des vitesses défini par :

Attention : Jet homocinétique à l'air libre
On considère l'écoulement stationnaire d'un fluide incompressible sous forme :
D'un jet libre, c'est-à-dire sans aucun contact avec une surface rigide ou un autre fluide
De vitesse constante

Ce jet est dit homocinétique.

On suppose que les seules forces intervenant sont les forces de pression ; la relation de Bernoulli s'écrit, dans tout le jet :

La vitesse étant la même en tout point du jet, il en est de même de la pression.
Aux bords du jet, au contact de l'atmosphère, la pression vaut
 . C'est donc la pression en tout point du jet.
. C'est donc la pression en tout point du jet.
Dans un jet homocinétique à l'air libre, la pression est uniforme et égale à celle existant dans le milieu extérieur.
On admettra ce résultat pour tout jet à l'air libre.





