Démarrage d'une automobile
Consacrer 10 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Le coefficient de frottement de la roue sur le sol est f. La roue a une masse m, un rayon R et un moment d'inertie J par rapport à son axe.
On lui applique un couple moteur :
\(\vec \Gamma _m = \Gamma _m \vec u_y\)
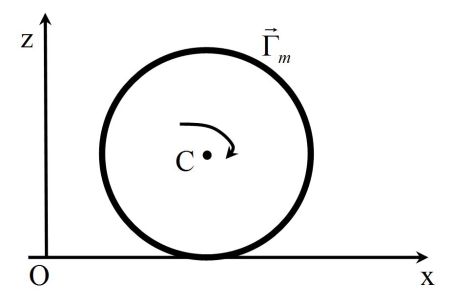
Question
Quelle est la condition sur \(\vec \Gamma _m\) pour qu'il y ait roulement sans glissement ?
Indice
Faire l'hypothèse de non glissement ; vérifier a posteriori que \(T<fN\).
Solution
Pour que la roue ne glisse pas sur le sol, il faut que T < fN.
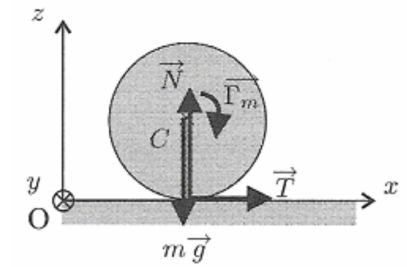
Le théorème de la résultante cinétique appliqué à la roue et projeté sur les axes Ox et Oz donne :
\(m\ddot x_C = T\) et \(0 = - mg + N\)
Le théorème du moment cinétique barycentrique appliqué à la roue et projeté donne :
\(J\dot \omega = - RT + \Gamma _m\)
La condition de roulement sans glissement donne :
\(\dot x_C - R\omega = 0\)
Après calculs, on peut extraire T sous la forme :
\(T = \frac{{\Gamma _m }}{{R\left( {1 + \frac{J}{{mR^2 }}} \right)}}\)
Et la condition T < fN donne alors :
\(\Gamma _m < fmgR\left( {1 + \frac{J}{{mR^2 }}} \right)\)