Interaction between a proton and a neutron
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
Let us study the interaction between a proton and a neutron.
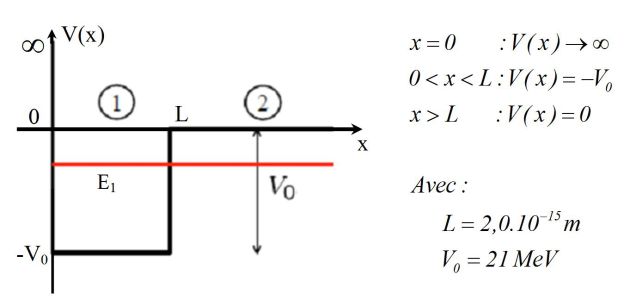
The following picture shows the simplified potential \(V(x)\) of the neutron in the field of the proton.
The potential only depends on the distance \(x\) between the neutron and the proton (located at the origin in \(x=0\)).
Only one bound state exists, for which the energy of the neutron is written \(E_1\).
The association of a proton and a neutron is a deuterium nucleus.
Question
Which interaction is responsible for the cohesion of the nucleus ?
Can you give an order of its magnitude ?
Why do heavy atoms have more neutrons than protons?
Solution
It is strong interaction.
To find an order of magnitude, let us evaluate for instance the electrostatic force between two protons and say the strong interaction is at least superior to the result found.
Strong interaction is the strongest among fundamental interactions. Its coupling constant is of approximately a hundred times greater than the electromagnetic interaction, a million times bigger than that of weak interaction, and \(10^{39}\) times more than the one of gravitation.
Conversely to other fundamental equations, the intensity of strong interaction does not diminish with the distance.
The heavy nuclei have more neutrons than protons in order to minimize electrostatic interaction.
Question
In the context of classic mechanics, qualitatively describe the movement of the neutron, and interpret the constant \(V_0\).
Solution
The neutron stays confined inside the well.
Question
The context is now quantum mechanics.
Let \(\varphi (x)\) be the probability amplitude of the neutron, which is solution to Schrödinger's equation :
\(- \frac{{{\hbar ^2}}}{{2m}}\frac{{{d^2}\varphi (x)}}{{d{x^2}}} + V(x)\varphi (x) = E\varphi (x)\)
Numeric values:
\(m = {1,67.10^{ - 27}}\;kg\) ; \(\hbar \approx {10^{ - 34}}\;J.s\)
Show that the probability amplitude \(\varphi (x)\) can be written as such :
\(\varphi (x) = \left\{ \begin{array}{l}A\sin kx\;\;\;\;\;\;\;\;\;\;(0 < x < L) \\C{e^{ - \alpha x}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(x > L) \\\end{array} \right.\)
\(k\) and \(\alpha\) are parameters to be expressed in function of the given data.
\(A\) and \(C\) are constants of integration that will not be determined.
Solution
Schrodinger's equation is, in both domains :
In region (1) :
\(\frac{{{d^2}\varphi (x)}}{{d{x^2}}} + k\varphi (x) = 0\;\;\;\;\;(k = \sqrt {2m({E_1} + {V_0})} /\hbar )\)
Or :
\(\varphi (x) = A\sin (kx) + B\cos (kx)\)
And \(\varphi (x=0)=0\), hence :
\(\varphi (x) = A sin(kx)\)
In region (2) :
\(\frac{{{d^2}\varphi (x)}}{{d{x^2}}} - {\alpha ^2}\varphi (x) = 0\;\;\;\;\;(\alpha = \sqrt {2m\left| {{E_1}} \right|} /\hbar )\)
And :
\(\varphi (x) = C{e^{ - \alpha x}} + D{e^{ + \alpha x}} \)
This solution does not diverge in infinity, so :
\(\varphi (x) = C{e^{ - \alpha x}}\)
Question
Prove that :
\(\alpha = - k\cot an(kL)\;\;\;\;\;\;\;and\;\;\;\;\;\;\;{\alpha ^2} + {k^2} = \frac{{2m{V_0}}}{{{\hbar ^2}}}\)
Solution
The wave function and its derivative are continuous in \(x = L\) :
\(\left\{ \begin{array}{l}A\sin (kL) = C{e^{ - \alpha L}} \\kA\cos (kL) = - \alpha C{e^{ - \alpha L}} \\\end{array} \right.\)
By computing the ratio :
\(\alpha = - k\cot an(kL)\)
And it can easily noticed that :
\({\alpha ^2} + {k^2} = \frac{{2m{V_0}}}{{{\hbar ^2}}}\)
Question
Deduce, by a graphic method, that only one bound state exists for the neutron, of energy \(E_1\) that will be determined.
Draw, without any prior calculation, the shape of the probability density as a function of \(x\).
Solution
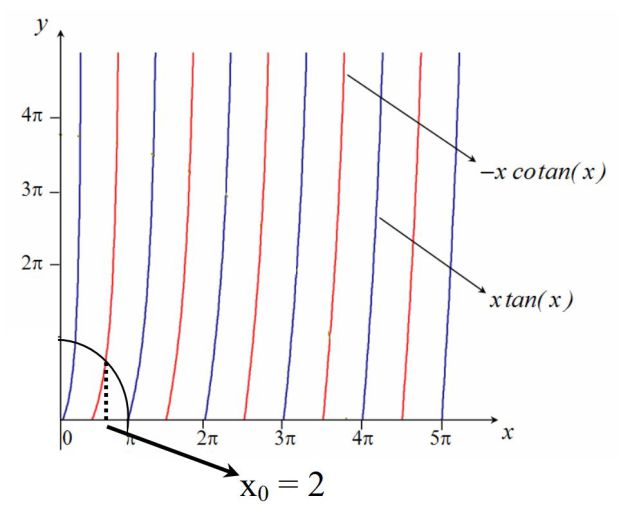
We can write :
\(\alpha L = - kL\cot an(kL)\)
And :
\({\left( {\alpha L} \right)^2} + {\left( {kL} \right)^2} = \frac{{2m{L^2}{V_0}}}{{{\hbar ^2}}} = {R^2} = 9\)
Let's write \(x=kL\) and \(y=\alpha L\) :
\(y = - x\cot an(x)\;\;\;\;\;and\;\;\;\;\;{x^2} + {y^2} = {R^2}\)
\(x_0\) is determined graphically and this can be deduced : \(x_0=2\)
We can evaluate the energy :
\(kL = \sqrt {2m({E_1} + {V_0})} L/\hbar = {x_0}\;\;\;\;\;so\;\;\;\;\;{E_1} \approx - 2,3\;MeV\)
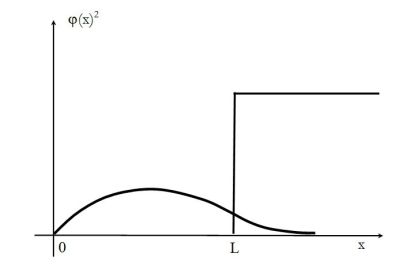
The density of probability is, without any computation, given in the figure above.
Question
Evaluate the order of magnitude of the temperature above which deuterium is no longer stable.
Solution
The temperature is in the order of :
\(- {E_1} \approx {k_B}T\;\;\;\;\;so\;\;\;\;\;T \approx \frac{{{{2,3.10}^{ - 13}}}}{{{{1,4.10}^{ - 23}}}} \approx 16\;milliards\;de\;K\)