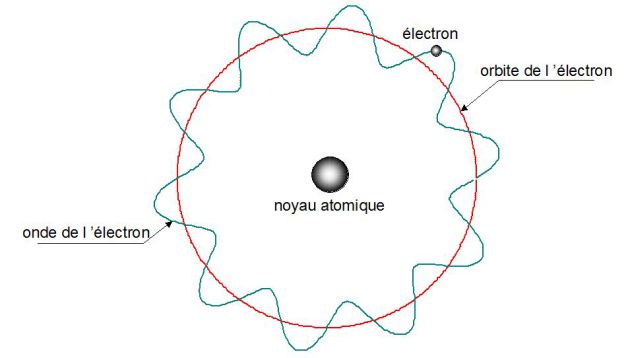
Bohr's model
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
The hydrogen atom is studied with Bohr's model.
It is made of a stationary proton in point O, chosen to be the origin, and of an electron in point M (its mass \(m\) and its charge \(-e\)).
The electron gravitates around the proton.
The distance between O and M is \(r=OM\) ; \(E\) is the total energy and \(v\) is the velocity of the electron.
We give :
\(\hbar \approx 10^{-34}J.s\) ; \(m \approx 10^{-30}kg\) ; \(1/4\pi \varepsilon_0 = 9.10^9 SI\).
Question
Write a condition of quantification between the De Broglie wavelength of the electron and the distance \(r\).
Deduce the quantification of the kinetic moment of the electron, in regard to the proton,\(\vec L_O\) , as \(L_O = n \hbar\)and \(n\) in a natural integer.
Solution
For the interferences not to be destructive, the wavelength of the orbit must be a multiple integer of the wavelength of the electron.
If \(R\) is the radius of the orbit, then :
\(2\pi R = n\lambda\)
Hence :
\(R=\frac {n \lambda}{2 \pi}\)
Only certain orbits can allow the existence of a wave (stationary wave) for the electron spinning around the nucleus.
Moreover, according to wave mechanics :
\(\lambda = \frac {h}{p}=\frac {h}{mv}\)
Hence :
\(mvR = n\frac{h}{{2\pi }}\)
It can be interpreted by saying that the kinetic moment of the electron regarding the proton is a multiple integer of the quantity \(\hbar = h/2\pi\). Naturally, Bohr's results are found.
Question
An action (written \(A\)) is a physical quantity of a system which has Planck's reduced constant for a unit.
For example, in the case of the hydrogen atom, the kinetic moment corresponds to an action.
Are the following systems classic or quantum ?
An hour-hand watch ?
An oscillating circuit, of capacitance \(0,1\) \(nF\) and inductance \(0,1\) \(mH\), which is travelled by an intensity of \(1\) \(mA\) ?
Solution
About the watch : the kinetic moment of the needle is around \(mL^2\Omega\).
\(m\) is around \(1\) gram, \(L\) is around \(1\) \(cm\) and is one revolution per minute, so the kinetic moment is equal to \(10^{-10}J.s\).
This is much bigger than \(h\) : the watch is not a quantum system.
About the oscillating circuit, the energy of the coil and an order of time, inverse of the frequency can be calculated.
A quantity homogenous to an action is found.
It is equal to \(3.10^{-17}J.s>>h\).
The circuit is not a quantum system.
Question
It has been proven that the energy and the radius of the electron are also quantified, and can be written :
\({E_n} = - \frac{{{E_0}}}{{{n^2}}}\;\;\;\;\;\;\;(with\;{E_0} = 13,6\;eV)\;\;\;\;\;and\;\;\;\;\;{r_n} = {n^2}{r_0}\;\;\;\;\;\;\;(with\;{r_0} = 50\;pm)\)
By doing an electric discharge in a light bulb filled with hydrogen gas (dihydrogen), the dihydrogen molecules dissociate.
The excited atoms emit electromagnetic radiation of different wavelengths.
Physicist J. Balmer determined experimentally that the wavelengths of this radiation belonged to the visible part of light, and verified the following phenomenological law :
\(\frac{1}{\lambda } = {R_H}\left[ {\left( {\frac{1}{4}} \right) - \left( {\frac{1}{{{n^2}}}} \right)} \right]\;\;\;\;\;\;\;\;(n = 3,\;4,\;5,\;...)\)
Where \(R_H\) (Rydberg's constant) is equal to \(109\) \(677\) \(cm^{-1}\).
In Bohr's model, determine \(R_H\) as a function of the given data.
Compute \(R_H\) numerically and compare it to the experimental value.
Solution
When a hydrogen atom goes from a level defined by the quantum number \(n\) to a level corresponding to a quantum level \(2\), it emits a photon which energy is :
\(h\nu = \frac{{hc}}{\lambda } = {E_n} - {E_2}\)
Consequently, the wave number (defined as the inverse of the wave length of the emitted radiation) is written :
\(\frac{1}{\lambda } = \frac{1}{{hc}}\left( {{E_n} - {E_2}} \right) = \frac{{{E_0}}}{{hc}}\left( {\frac{1}{4} - \frac{1}{{{n^2}}}} \right)\)
Rydberg's constant can be interpreted like the quantity :
\({R_H} = \frac{{{E_0}}}{{hc}} = {1,09.10^7}{m^{ - 1}} = {1,09.10^5}c{m^{ - 1}}\)
The theoretical value matches very well the experimental value given by J. Balmer.
Question
The electron, which has an accelerated movement around the proton, emits an electromagnetic radiation and loses energy.
Larmor's formula gives the power emitted by the electron, where \(a\) is its acceleration and \(c\) the speed of light in empty space :
\(P = \frac{2}{3}\frac{{{e^2}}}{{4\pi {\varepsilon _0}{c^3}}}{a^2}\)
Suppose the electron is in its fundamental state \(n = 1\).
Give the order of magnitude of the energy lost by the electron during one rotation.
In this question, the trajectory of the electron is supposed to be circular and uniform.
\(r(t)\) is the radius of the electron at instant \(t\).
Show that it verifies the following differential equation by using an approximation which will be specified :
\(\frac{{dr(t)}}{{dt}} = - \frac{4}{3}\frac{1}{{{m^2}{c^3}}}{\left( {\frac{{{e^2}}}{{4\pi {\varepsilon _0}}}} \right)^2}\frac{1}{{r{{(t)}^2}}}\)
Estimate how much time it will take to the electron to fall on the proton. Comment this result.
Solution
The acceleration of the electron is \(a=v_0^2/r_0\). The trajectory is circular :
\(ma = m\frac{{v_0^2}}{{{r_0}}} = \frac{{{e^2}}}{{4\pi {\varepsilon _0}}}\frac{1}{{r_0^2}}\;\;\;\;\;\;\;so\;\;\;\;\;\;\;a = \frac{{{e^2}}}{{4\pi {\varepsilon _0}m}}\frac{1}{{r_0^2}}\;\;\;\;\;and\;\;\;\;\;v_0^{} = \sqrt {\frac{{{e^2}}}{{4\pi {\varepsilon _0}m}}\frac{1}{{r_0^{}}}}\)
The power is :
\(P = \frac{2}{3}\frac{{{e^2}}}{{4\pi {\varepsilon _0}{c^3}}}{\left( {\frac{{{e^2}}}{{4\pi {\varepsilon _0}m}}\frac{1}{{r_0^2}}} \right)^2}\)
In order of magnitude :
\({v_0} \approx {10^6}m.{s^{ - 1}}\;;\;{T_0} \approx {3.10^{ - 16}}s\;;\;P \approx {10^{ - 7}}W\;and\;\delta E = P{T_0} \approx {3.10^{ - 23}}J\)
The relative variation of energy is :
\(\frac {\delta E}{E_0} \approx 10^{-5}\)
The trajectory is a spiral : the radius \(r(t)\) diminishes very slowly in function of time.
The trajectory can be supposed as almost circular.
The energy on the near-circular trajectory is :
\(E(t) = - \frac{1}{2}\frac{{{e^2}}}{{4\pi {\varepsilon _0}}}\frac{1}{{r(t)}}\)
And :
\(\frac{{dE(t)}}{{dt}} = \frac{1}{2}\frac{{{e^2}}}{{4\pi {\varepsilon _0}}}\frac{{\dot r(t)}}{{r{{(t)}^2}}} = - P = - \frac{2}{3}\frac{{{e^2}}}{{4\pi {\varepsilon _0}{c^3}}}{\left( {\frac{{{e^2}}}{{4\pi {\varepsilon _0}m}}\frac{1}{{r{{(t)}^2}}}} \right)^2}\)
Hence the differential equation :
\(\frac{{dr(t)}}{{dt}} = - \frac{4}{3}\frac{1}{{{m^2}{c^3}}}{\left( {\frac{{{e^2}}}{{4\pi {\varepsilon _0}}}} \right)^2}\frac{1}{{r{{(t)}^2}}}\)
After integration :
\({r^3} - r_0^3 = - {\left( {\frac{{{e^2}}}{{4\pi {\varepsilon _0}}}} \right)^2}\frac{4}{{{m^2}{c^3}}}t\)
The duration is :
\({t_f} = \frac{{{m^2}{c^3}}}{4}{\left( {\frac{{4\pi {\varepsilon _0}}}{{{e^2}}}} \right)^2}r_0^3 \approx 0,5\;ns\)
The radius of the trajectory of the electron around the nucleus inexorably diminishes.
The model proposed for the hydrogen atom does not lead to a stable system.
Only the quantum mechanics theory can overcome this difficulty.