Oscillations transversales d'une corde plombée
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
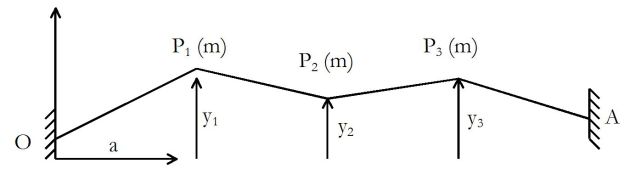
Une corde élastique de masse négligeable est, à l'équilibre, tendue avec une force F entre deux points fixes O et A distants de 4a.
La corde porte, régulièrement espacés, trois plombs P1, P2 et P3 de même masse m.
On néglige le poids des plombs, chaque tronçon de corde dont la longueur est a dans l'état d'équilibre initial est caractérisé par la raideur k et la longueur naturelle \(\ell_0<a\).
On pose \(\omega_0^2=F/ma\).
On étudie les petits mouvements transversaux des plombs ; l'ordonnée du plomb Pn est yn à la date t (yn << a), on admet que son abscisse reste constamment égale à xn = na.
Question
Établir un système différentiel du second ordre relatif au mouvement étudié.
Indice
Appliquer le PFD à chacun des plombs.
Rappelez-vous, les amplitudes sont faibles.
Solution
Le PFD appliqué à chaque plomb en projection verticale donne :
\(\begin{array}{l}m\ddot y_1 = - F\frac{{y_1 }}{a} - F\frac{{y_1 - y_2 }}{a} \\m\ddot y_2 = F\frac{{y_1 - y_2 }}{a} - F\frac{{y_2 - y_3 }}{a} \\m\ddot y_3 = - F\frac{{y_3 - y_2 }}{a} - F\frac{{y_3 }}{a} \\\end{array}\)
Soit :
\(\begin{array}{l}\ddot y_1 = \omega _0^2 ( - 2y_1 + y_2 ) \\\ddot y_2 = \omega _0^2 (y_1 - 2y_2 + y_3 ) \\\ddot y_3 = \omega _0^2 (y_2 - 2y_3 ) \\\end{array}\)
Question
On recherche des solutions du type \(y_n=a_ncos\omega t\) (tous les plombs vibrant en phase à la même fréquence).
Déterminer les valeurs de ω possibles pour de tels mouvements (modes propres du système).
Solution
On obtient le système linéaire :
\(\begin{array}{l}(\omega ^2 - 2\omega _0^2 )a_1 + \omega _0^2 a_2 = 0 \\\omega _0^2 a_1 + (\omega ^2 - 2\omega _0^2 )a_2 + \omega _0^2 a_3 = 0 \\\omega _0^2 a_2 + (\omega ^2 - 2\omega _0^2 )a_3 = 0 \\\end{array}\)
Ce système ne possède de solutions non triviales que si son déterminant est nul :
\(\left| \begin{array}{l}\omega ^2 - 2\omega _0^2 \;\;\;\;\;\;\;\;\;\omega _0^2 \;\;\;\;\;\;\;\;\;\;\;\;0 \\\;\;\;\;\;\omega _0^2 \;\;\;\;\;\;\;\;\omega ^2 - 2\omega _0^2 \;\;\;\;\;\;\;\omega _0^2 \;\; \\\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;\;\omega _0^2 \;\;\;\;\;\;\;\;\omega ^2 - 2\omega _0^2 \\\end{array} \right|\; = \;0\)
On obtient alors trois pulsations propres :
\(\omega _1 = \omega _0 \sqrt {2 - \sqrt 2 } \;\;\;\;\;;\;\;\;\;\;\omega _2 = \omega _0 \sqrt 2 \;\;\;\;\;;\;\;\;\;\;\omega _3 = \omega _0 \sqrt {2 + \sqrt 2 }\)