Écoulement autour d'un cylindre
(10 minutes de préparation)
Un cylindre de rayon R et en rotation uniforme à la vitesse angulaire \(\omega\) autour de son axe (Oz) vertical est placé dans l'air dont l'écoulement loin du cylindre se fait avec une vitesse uniforme \(\vec U = U\vec e_x\) et à la pression \(P_0\).
L'air est considéré comme un fluide incompressible, de masse volumique \(\rho\), en écoulement stationnaire, et supposé parfait.
L'action de la pesanteur sur l'air est négligée.
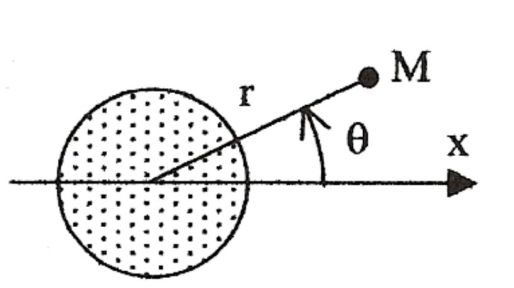
Les coordonnées polaires de la vitesse \(\vec v\) de cet écoulement sont :
\(v_r = \left( {1 - \frac{{R^2 }}{{r^2 }}} \right)U{\kern 1pt} \cos \theta \;\;\;\;\;;\;\;\;\;\;v_\theta = - \left( {1 + \frac{{R^2 }}{{r^2 }}} \right)U{\kern 1pt} \sin \theta + \frac{\Gamma }{{2\pi r}}\)
Avec \(\Gamma\) une constante algébrique appelée intensité du tourbillon et reliée à \(\omega\) par la relation :
\(\Gamma = 2 \pi R^2 \omega\)
Question
Pour créer un tel écoulement, on part d'un cylindre initialement immobile dans l'air, puis on le soumet à une accélération angulaire pour lui communiquer finalement la vitesse angulaire constante \(\omega\) et arriver au régime d'écoulement décrit ci - dessus.
Cela est-t-il compatible avec les hypothèses précédentes sur l'air ?
Question
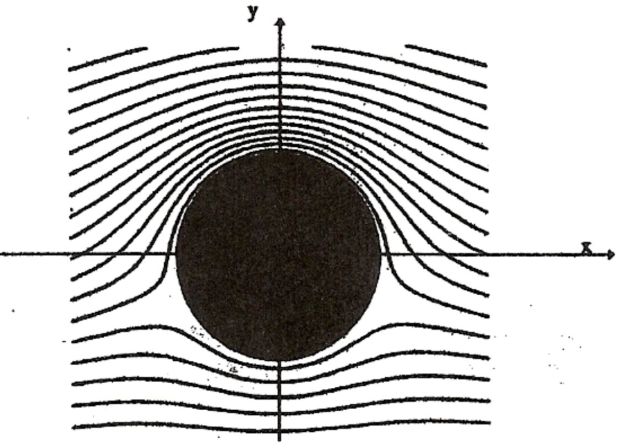
On donne le tracé des lignes de courant pour un choix de valeurs de U, R et \(\Gamma\).
Comparer qualitativement le module \(v\) de la vitesse du fluide pour les points situés sur l'axe (Oy) selon \(y>R\) ou \(y<-R\).
Indiquer le signe de \(\Gamma\).
La figure montre l'existence de points d'arrêts du fluide à la surface du cylindre pour \(\theta_1=-30°\) et \(\theta_2=-150°\), préciser ce qui permet de les situer.
En déduire l'expression de \(\Gamma\) en fonction de U et de R.
Question
Déterminer la pression \(P(\theta )\) à la surface du cylindre.
Question
Déterminer, sans faire de calcul, en observant la forme de \(P(\theta)\), la valeur de la composante \(F_x\) de la force appliquée sur le cylindre. Commenter le résultat.
Justifier, sans calcul, l'existence d'une portance.
Indiquer son effet sur le cylindre et les applications éventuelles.