La dynamo-disque homopolaire
(20 minutes de préparation)
Une dynamo est constituée :
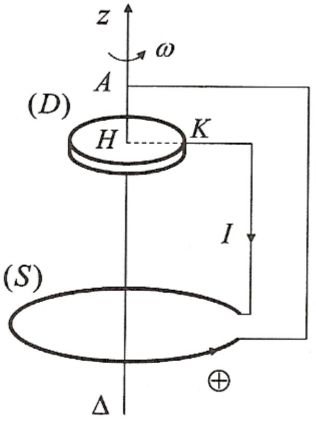
D'un disque conducteur (D) de rayon \(a\), de moment d'inertie \(J\) par rapport à son axe \(\Delta\) autour duquel il tourne avec la vitesse angulaire \(\omega\).
Il est soumis à un couple mécanique constant \(\Gamma\).
On suppose que le courant circule dans (D) suivant un rayon unique HK.
D'un bobinage métallique représenté sur le dessin par une spire circulaire unique (S) d'axe \(\Delta\) et reliée à l'axe (point A) et à la périphérie du disque (point K) par un fil conducteur qui ferme le circuit.
\(R\) et \(L\) désignent la résistance et l'inductance propre du circuit complet.
On rappelle que si \(I\) désigne le courant dans le circuit et :
\(\vec B = B_z\vec u_z+B_r\vec u_r\)
le champ magnétique créé par le bobinage au niveau du disque, le coefficient d'inductance mutuelle entre (S) et la périphérie de (D) est défini à l'aide du flux :
\(\Phi=\iint_D \vec B.d\vec S=\int_0^a B_z2\pi rdr=MI\)
Un document sur l'origine du champ magnétique terrestre et la géodynamo
Question
1. Exprimer en fonction de \(M\), \(I\) et \(\omega\) la fém \(e_{HK}\) existant entre l'axe et la périphérie de (D) et en déduire l'équation électrique (1) du circuit.
Question
2. Exprimer en fonction de \(M\) et de \(I\) le couple \(\vec \Gamma_L\) des forces de Laplace s'appliquant à (D) et en déduire l'équation mécanique (2) du circuit.
Question
3. Effectuer le bilan de puissance instantanée du système, pris en valeur moyenne en supposant qu'un régime périodique puisse s'établir et dégager l'intérêt de ce dispositif.
Comment peut-on utiliser ce principe de dynamo pour expliquer l'origine du champ magnétique terrestre ?