Pince ampèremétrique
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Les ampèremètres usuels ne supportent pas les fortes intensités (en général, Imax = 10 A).
Pour mesurer des intensités supérieures, on utilise une pince ampèremétrique, dont on va étudier le principe.
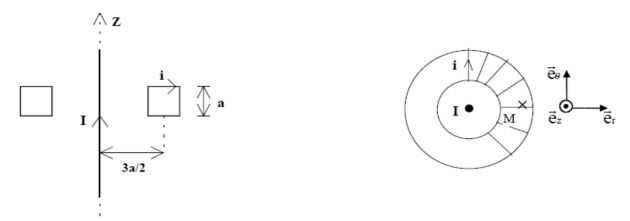
Un fil rectiligne infini d'axe (Oz) est parcouru par un courant (c'est le courant à mesurer) d'intensité :
\(I(t)=I_{max} cos(\omega t)\)
On entoure le fil d'un bobinage constitué d'un tore de section carrée de côté a et de rayon moyen 3a / 2, sur lequel sont régulièrement enroulées un grand nombre de spires N.
Ce bobinage est fermé sur un ampèremètre, le circuit ainsi réalisé a une résistance totale R et est parcouru, par induction, par un courant sinusoïdal :
\(i(t)=i_{max} cos(\omega t+\phi)\)
Question
Calculer la fém induite par le courant I(t).
Indice
Il y a deux champs magnétiques et donc deux flux à calculer.
Solution
Le champ magnétique dû au fil infini en un point intérieur au tore est :
\(\vec B_{fil} = \frac{{\mu _0 I(t)}}{{2\pi }}\frac{1}{r}\vec u_\theta\)
Celui propre au tore est (appliquer le théorème d'Ampère) :
\(\vec B_{tore} = \frac{{\mu _0 Ni(t)}}{{2\pi }}\frac{1}{r}\vec u_\theta\)
Le champ total est donc :
\(\vec B = \frac{{\mu _0 }}{{2\pi }}\left( {Ni(t) + I(t)} \right)\frac{1}{r}\vec u_\theta\)
Le flux de ce champ à travers les N spires du tore vaut alors :
\(\Phi = N = \frac{{N\mu _0 }}{{2\pi }}\left( {Ni(t) + I(t)} \right)a\ln 2\)
On en déduit la fém en utilisant la loi de Faraday :
\(e = - \frac{{d\phi }}{{dt}} = - \frac{{N\mu _0 }}{{2\pi }}\left( {N\frac{{di(t)}}{{dt}} + \frac{{dI(t)}}{{dt}}} \right)a\ln 2\)
Question
Calculer le rapport
\(\frac{{i_{\max } }}{{I_{\max } }}\)
On pourra négliger R devant \(\mu _0 \omega aN^2\) .
Solution
L'équation électrique du circuit est alors :
\(e = - \frac{{N\mu _0 }}{{2\pi }}\left( {N\frac{{di(t)}}{{dt}} + \frac{{dI(t)}}{{dt}}} \right)a\ln 2 = Ri\)
Soit, en notation complexe :
\(- \frac{{N\mu _0 }}{{2\pi }}\left( {N\underline i (t) + \underline I (t)} \right)j\omega a\ln 2 = R\underline i\)
D'où :
\(\frac{{\underline i (t)}}{{\underline I (t)}} = \frac{{ - j\omega \frac{{\mu _0 }}{{2\pi }}Na\ln 2}}{{R + j\omega \frac{{\mu _0 }}{{2\pi }}N^2 a\ln 2}}\)
On peut négliger R devant \(\mu _0 \omega aN^2\) ;
\(\frac{{\underline i (t)}}{{\underline I (t)}} = \frac{1}{N}\)
Avec N de l'ordre de \(10^4\), on peut mesurer de fortes intensités avec des ampèremètres de faible calibre.