Quantité d'électricité induite
(15 minutes de préparation)
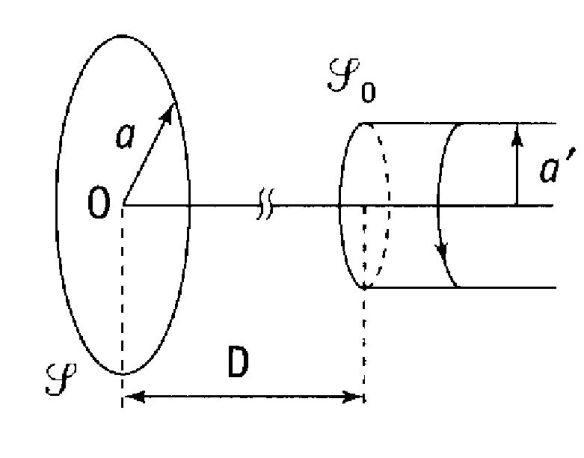
(S) est une spire de centre 0 et de rayon a. Elle possède une résistance R et un coefficient d'auto-inductance L.
(S0) est un solénoïde « semi - infini », de rayon a', comportant n spires par unité de longueur. L
es axes de (S) et (S0) sont communs et le point O est situé à une distance D de la face d'entrée du solénoïde.
Dans toute la suite, on supposera que l'on a :
D » a' et D » a.
Le coefficient de mutuelle entre (S) et (S0) est donné par :
\(M = \frac{{\mu _0 n\ \pi \ a^2 a'^2 }}{{4\ D^2 }}\)
On crée un courant I constant dans le solénoïde.
Question
Déterminer la quantité totale d'électricité q qui aura traversé toute section du fil constituant la spire. Commenter.
Solution
Quand on crée le courant I dans le solénoïde, il apparaît un flux variable à travers la spire.
On note i' le courant dans le solénoïde, variant de 0 à I sur une durée \(\tau\). Si i est le courant dans la spire (S), alors la fém qui se crée est donnée par la loi de Fraday :
\(e = - \frac{{d\phi '}}{{dt}} = - M\frac{{di'}}{{dt}} = Ri + L\frac{{di}}{{dt}}\)
On intègre en 0 et \(\tau\) :
\(- M\int_0^\tau {di'} = \int_0^\tau {Ridt} + \int_0^\tau {Ldi} = \int_0^\tau {Rdq} + \int_0^\tau {Ldi}\)
Soit, avec \(i(\tau ) = i(0) = 0\) et \(i'(\tau )=I\) :
\(- MI = Rq_{ind} \;\;\;\;\;soit\;\;\;\;\;q_{ind} = - \frac{M}{R}I\)
On remarque que qind < 0 : le signe – est lié à i < 0 (loi de Lenz).
Question
On suppose que le courant I est créé à partir de t = 0 de façon « suffisamment rapide ». Préciser.
Quelle est alors l'expression du courant i(t > 0) circulant dans La spire ? Commenter.
Solution
La spire est caractérisée par L et R (temps caractéristique \(\tau _c = L/R\)). On suppose que \(\tau <<\tau_c \). On repart alors de :
\(- M\frac{{di'}}{{dt}} = Ri + L\frac{{di}}{{dt}}\)
Que l'on intègre entre 0 et \(\tau =0^+<<\tau_c \), afin d'obtenir en quelque sorte une condition initiale :
\(- MI = \int_0^\tau {Ridt} + L\left( {i(\tau ) - i(0)} \right)\)
D'où :
\(i(\tau ) = - \frac{{MI}}{L}\)
On a considéré que :
\(\int_0^\tau {Ridt} = Rq(\tau ) \to 0\) quand \(\tau\) tend vers 0.
Pour \(t>\tau =0^+\), l'équation différentielle vérifiée par i est simplement :
\(Ri + L\frac{{di}}{{dt}} = 0\)
D'où :
\(i(t) = - \frac{{MI}}{L}e^{ - t/\tau _c }\)
On peut retrouver la quantité de charge induite :
\(q_{ind} = - \frac{{MI}}{L}\int_0^\infty {e^{ - t/\tau _c } dt} = - \frac{{MI}}{R}\)