Thermomètre à affichage numérique
(10 minutes de préparation)
Le principe d'un thermomètre à affichage numérique est le suivant :
La sonde thermométrique est une résistance de platine, dont la résistance RPt varie avec la température selon la loi
\(R_{Pt}=R_{Pt,0}(1+\alpha t)\)
Où t est la température exprimée en °C, \(\alpha\) le coefficient de température de résistivité (\(\alpha=4,00.10^{-3}.C^{-1}\)), RPt la résistance en Ω à la température t et RPt,0 la résistance en Ω à 0°C (\(R_{Pt,0}=1,00.10^2\;\Omega\)).
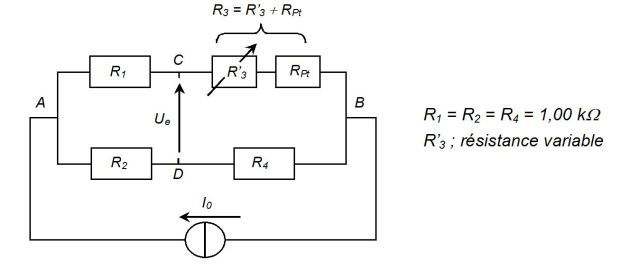
Ce capteur est placé dans une des branches d'un pont de mesures (pont de Wheastone) alimenté par un générateur idéal de courant continu (\(I_0=1,00\;mA\)).
Les résistances R1, R2, R'3 et R4 sont supposées être indépendantes de la température.
Question
Déterminer la tension \(U_e\) en fonction de \(I_0\), \(R_1\), \(R_2\), \(R_3=R'_3+R_{Pt}\) et \(R_4\).
Solution
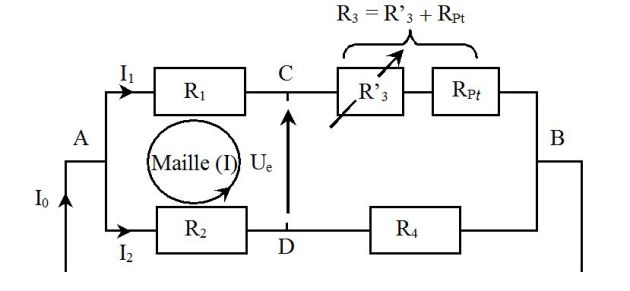
La loi des mailles appliquée à la maille (I) définie sur la figure ci-dessus donne :
\({U_e} = - {R_1}{I_1} + {R_2}{I_2}\)
Or, d'après la règle du diviseur de courant :
\({I_1} = \frac{{{R_2} + {R_4}}}{{{R_1} + {R_2} + {R_3} + {R_4}}}{I_0}\)
Et :
\({I_2} = \frac{{{R_1} + {R_3}}}{{{R_1} + {R_2} + {R_3} + {R_4}}}{I_0}\)
En reportant dans l'expression de Ue, on obtient finalement :
\({U_e} = \frac{{{R_2}{R_3} - {R_1}{R_4}}}{{{R_1} + {R_2} + {R_3} + {R_4}}}{I_0}\)
Question
Quelle valeur faut-il donner à \(R'_3\) si le pont est équilibré à \(t=0°C\), c'est-à-dire si \(U_e=0\) à cette température ?
\(R'_3\) gardera cette valeur dans la suite de l'exercice.
Solution
Pour que le pont soit équilibré à la température de 0°C, il faut que :
\({R_2}{R_3} = {R_1}{R_4}\)
Soit :
\(R{'_3} = \frac{{{R_1}{R_4}}}{{{R_2}}} - {R_{Pt,0}} = 900\,\Omega\)
Question
La température pouvant varier entre 0°C et 50°C, déterminer \(U_e\) en fonction de la température t.
Faire l'application numérique pour \(t=0°C\), \(10°C\), \(20°C\), \(30°C\), \(40°C\) et \(50°C\).
\(U_e\) varie-t-elle linéairement en fonction de la température t ?
Solution
A une température t quelconque (exprimée en °C), la résistance de platine peut s'exprimer sous la forme :
\({R_{Pt}} = {R_{Pt,0}} + \alpha {R_{Pt,0}}\,t\)
La tension Ue peut alors s'écrire :
\({U_e} = \frac{{{R_2}(R{'_3} + {R_{Pt,0}} + \alpha {R_{Pt,0}}\,t) - {R_1}{R_4}}}{{{R_1} + {R_2} + R{'_3} + {R_{Pt,0}} + \alpha {R_{Pt,0}}\,t + {R_4}}}{I_0}\)
Par conséquent, en utilisant la condition d'équilibre du pont à 0°C :
\({U_e} = \,\,\,\frac{{\alpha {R_{Pt,0}}\,t}}{{{R_1} + {R_2} + R{'_3} + {R_{Pt,0}} + {R_4} + \alpha {R_{Pt,0}}\,t}}{R_2}{I_0}\)
Numériquement, il vient :
\({U_e} = \frac{{{{4.10}^{ - 1}}\,t}}{{4\,000 + {{4.10}^{ - 1}}\,t}} = \frac{t}{{t + 10\,000}}\)
Avec \(t\) en °C et \(U_e\) en V.
Les valeurs de la tension \(U_e\) pour les températures proposées dans l'énoncé sont répertoriées dans le tableau ci-dessous :
Température t (°C) | 0 | 10 | 20 | 30 | 40 | 50 |
Tension \(U_e\) (V) | 0 | \(10^{-3}\) | \(2.10^{-3}\) | \(3.10^{-3}\) | \(4.10^{-3}\) | \(5.10^{-3}\) |
On constate que, dans l'intervalle de températures considéré, \(t<<10000\) et que, par conséquent, \(U_e \approx 10^{-4}\;t\): la tension \(U_e\) varie de manière linéaire avec la température.
Question
Le signal \(U_e\) délivré étant faible, il est amplifié. Quel montage amplificateur peut-on utiliser ? Après amplification et mise en forme, on obtient la tension \(U_s\) :
\(t = 12,5({U_s} - 1)\)
Avec \(t\) en °C et \(U_s\) en V.
Solution
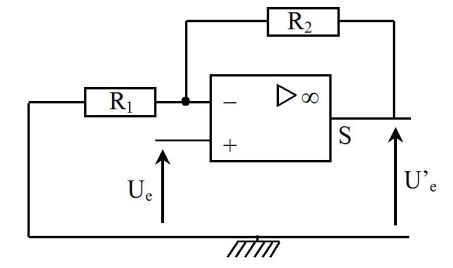
Un montage amplificateur simple peut, par exemple, être un montage amplificateur non inverseur, réalisé à partir d'un amplificateur opérationnel idéal et dont le schéma est rappelé sur la figure ci-dessous et pour lequel :
\(\frac{{U{'_e}}}{{{U_e}}} = 1 + \frac{{{R_2}}}{{{R_1}}}\)
Dans le cadre de cet exercice, la variation affine entre t et \(U_s\) est :
\(t = 12,5({U_s} - 1)\)
Avec \(t\) en °C et \(U_s\) en V.
Question
La tension \(U_s\) est appliquée à un convertisseur analogique-numérique (CAN) à approximations successives – 8 bits – échelle (0 – 5 V).
Le CAN permet de coder la tension analogique \(U_s\) en un nombre de 8 chiffres binaires (8 bits).
La caractéristique de transfert est donnée sur la figure ci-dessous.
Pourquoi utilise-t-on la base 2 et non la base 10 ? Combien de valeurs numériques le CAN peut-il distinguer ?
Quelle est la variation minimale \(\Delta U_s\) de \(U_s\) pour que la valeur numérique N en base 2 soit modifiée d'une unité, c'est-à-dire du bit de poids le plus faible ?
En déduire la variation minimale de température \(\Delta t\) que l'on peut apprécier avec ce montage.
Solution
La base 2 est utilisée ici car c'est elle qui, d'une manière générale, est utilisée en électronique logique.
Le nombre N comporte 8 chiffres, qui peuvent être égaux à 0 ou à 1. Par conséquent, N peut prendre \(2^8=256\) valeurs.
La variation minimale de la tension \(U_s\) que l'on pourra déceler sera alors donnée par :
\(\Delta {U_s} = 4/256 = {1,56.10^{ - 2}}V = 15,6\,mV\)
Ce qui correspond à une variation minimale de température égale à :
\(\Delta t = 12,5\Delta {U_s} \approx 0,20^\circ C\)