Charge d'un condensateur à l'aide d'une source de tension
Consacrer 10 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Pour t < 0, le circuit est au repos et e(t) est un échelon d'amplitude E.
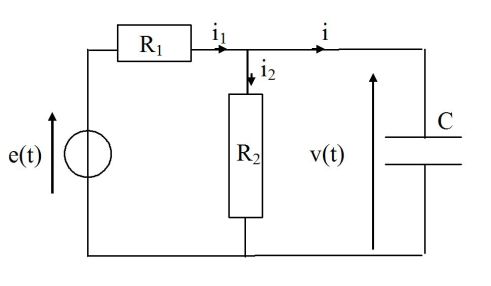
Question
On s'intéresse à l'état du circuit juste après l'application de la tension E ; déterminer i1(0+), i2(0+), i(0+) et v(0+).
Solution
On sait que la tension et la charge d'un condensateur sont des fonctions continues. Par conséquent :
\(v({0^ + }) = v(\left( {{0^ - }} \right) = 0\;\;\;\;\;;\;\;\;\;\;{i_2}({0^ + }) = \frac{{v({0^ + })}}{{{R_2}}} = 0\)
La loi des mailles et la loi des nœuds donnent ensuite :
\({i_1}({0^ + }) = i({0^ + }) = \frac{E}{{{R_1}}}\)
Question
On s'intéresse au régime permanent ; déterminer i1(+∞), i2(+∞), i(+∞) et v(+∞).
Solution
En régime permanent, i = 0, alors :
\({i_1}(\infty ) = {i_2}(\infty ) = \frac{E}{{{R_1} + {R_{_2}}}}\;\;\;\;\;et\;\;\;\;\;v(\infty ) = {R_2}{i_2}(\infty ) = \frac{{{R_2}}}{{{R_1} + {R_{_2}}}}E\)
Question
Déterminer l'expression de v(t).
Solution
En transformant le générateur de tension par un générateur de courant et en regroupant ensuite les résistances en parallèle, on se ramène, grâce à une nouvelle transformation en modèle de Thévenin, à un circuit série alimenté par un générateur de fem :
\({E_{eq}} = \frac{{{R_2}}}{{{R_1} + {R_2}}}E\)
En série avec une résistance :
\({R_{eq}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
La tension aux bornes du condensateur est alors :
\(v(t) = {E_{eq}}(1 - {e^{ - t/{R_{eq}}C}})\)
Question
Faire un bilan énergétique.
Solution
Le bilan énergétique s'écrit :
\(\int_0^\infty {E{i_1}(t)dt} = \frac{1}{2}Cv{(t)^2} + \int_0^\infty {{R_1}i_1^2(t)dt} + \int_0^\infty {{R_2}i_2^2(t)dt}\)