Power in electrokinetic
Fondamental : Definition of power in receptor convention
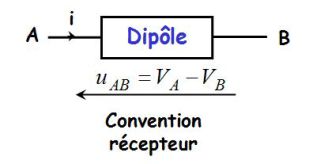
The electrical power received by the dipole (in receptor convention) is :
\(p = {u_{AB}}i\)
The energy \(\delta W\) received during the time interval \(dt\) is such that :
\(p = \frac{{\delta W}}{{dt}}\;\;\;\;\;so\;\;\;\;\;\delta W = pdt = {u_{AB}}i\;dt\)
Fondamental : Conductor and Joule's efficient
For an ohmic conductor :
\(p = {u_{AB}}i = R{i^2}\)
The electric power received by the conductor is then dissipated as heat to the outside (principle electric heaters).
Fondamental : Average power in forced sinusoidal
The voltage across the dipole (AB) can be written :
\(u_{AB}=U_{max}cos(\omega t)=U_{eff}\sqrt{2}cos(\omega t)\)
And intensity :
\(i=I_{max}cos(\omega t+\varphi)=I_{eff}\sqrt{2}cos(\omega t+\varphi)\)
Where \(\varphi\) is the phase shift of the intensity with respect to the voltage.
The instantaneous power received by the dipole AB is (in receptor convention) :
\(p(t) = u_{AB}i = {U_{\max }}{I_{\max }}\cos \omega t\cos (\omega t + \varphi ) = 2{U_{eff}}{I_{eff}}\cos \omega t\cos (\omega t + \varphi )\)
Let (with \(\cos a.\cos b = \frac{1}{2}\left( {\cos (a + b) + \cos (a - b)} \right)\)) :
\(p(t) = {U_{eff}}{I_{eff}}\left[ {\cos (2\omega t + \phi ) + \cos (\varphi )} \right]\)
And \(p(t)\) is a sinusoidal function of angular frequency \(2\omega\) and therefore of period \(T/2\).
The average power is calculated :
\(P = \frac{1}{T}\int_0^T {p(t)dt}\)
Is :
\(P = \frac{1}{T}{U_{eff}}{I_{eff}}\left( {\int_0^T {\cos (2\omega t + \varphi )dt} + \int_0^T {\cos (\varphi )dt} } \right)\)
Whence :
\(P = {U_{eff}}{I_{eff}}\cos (\varphi )\)
The term \(cos\varphi\) is called "power factor" : it depends on the impedance of the dipole AB.
Special cases of dipoles :
For resistance :
\(P = {U_{eff}}{I_{eff}} = RI_{eff}^2\;\;\;\;(\cos \varphi = 1)\)
For perfect coil :
\(P = 0\;\;\;\;(\cos \varphi = 0\;because\;\varphi = - \pi /2)\)
For a capacitor :
\(P = 0\;\;\;\;(\cos \varphi = 0\;because\;\varphi = \pi /2)\)
In a series circuit (RLC) :
\(\cos \varphi = \frac{R}{Z}\;\;\;and\;\;\;{U_{eff}} = Z{I_{eff}}\;\;\;\;\;so\;\;\;\;\;P = (Z{I_{eff}}){I_{eff}}(\frac{R}{Z})\)
So :
\(P = RI_{eff}^2\)
It's well verified that the power is entirely dissipated in the resistor.
For a complex impedance dipole \( \underline z = R + jS\) :
\(\underline u = (R + jS)\underline i \;\;\;so\;\;\;\;{U_{eff}} = (R + jS){I_{eff}}{e^{j\varphi }}\;\;\;\;and \;\;\;\;P = RI_{eff}^2\)
Only the real part of the impedance (necessarily positive) involved.
For admittance complex dipole \(\underline y = G + jB\) :
\(\underline i = (G + jA)\underline u \;\;\;so\;\;\;\;{I_{eff}}{e^{j\varphi }} = (G + jA){U_{eff}}\;\;\;\;and\;\;\;\;P = GU_{eff}^2\)
Only the real part of the admittance (necessarily positive) involved.
Fondamental : Importance of power factor
The power factor is the term \(cos\varphi\).
If the tension imposed, RMS current \(I_{eff}\) required to achieve a given power in a dipole is :
\({I_{eff}} = \frac{P}{{{U_{eff}}\cos \varphi }}\)
It will be all the weaker as the power factor is close to \(1\).
Or decrease the intensity reduces losses by Joule effect in the wires, from generators to the users circuits ; hence the importance to only supply high power factor circuit (usually, \(cos\varphi >0,9\)).
Complément : Adaptation of impedances
A stereo system (generator) is connected to the speakers (complex impedance \(\underline {z}_u\)).
How to choose the speaker impedance for the power received by them to be maximum ?
In this case, we say that there is adaptation of impedance.
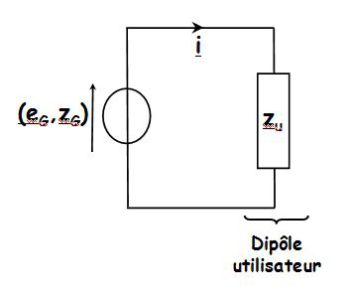
We denote :
\({\underline z _G} = {R_G} + j{A_G}\;\;\;\;and\;\;\;\;{\underline z _u} = {R_u} + j{A_u}\)
The average power received by the user dipole is :
\({P_u} = {R_u}I_{eff}^2\;\;\;\;\;with\;\;\;\;\;{I_{eff}} = \frac{{{E_{g,eff}}}}{{\sqrt {{{({R_u} + {R_G})}^2} + {{({A_u} + {A_G})}^2}} }}\)
Is :
\({P_u} = \frac{{{R_u}E_{g,eff}^2}}{{{{({R_u} + {R_G})}^2} + {{({A_u} + {A_G})}^2}}}\)
How to maximize \(P_u\), with \(E_{g,eff}\), \(R_G\) and \(A_G\) fixed (characteristics of the generator) ?
Have been shown \(R_G\) and \(R_u\) were necessarily positive, while \(A_G\) and \(A_u\) may be a priori \(<0\) (capacitive circuit) or \(>0\) (inductive circuit). So :
\(A_u=-A_G\)
is then chosen to minimize the denominator of \(P_u\).
Expression of power becomes :
\(\;{P_u} = \frac{{{R_u}E_{g,eff}^2}}{{{{({R_u} + {R_G})}^2}}}\)
It will be maximum if :
\(\frac{{d{P_u}}}{{d{R_u}}} = 0\;\;\;\;\;\;so\;\;\;\;\;{R_u} = {R_G}\)
The impedances are then complex conjugate :
\({\underline z _u} = {R_u} + j{A_u} = {R_G} - j{A_G} = {\underline {\overline z } _G}\)
There is talk of adaptation of impedance.
The maximum power is equal to :
\(\;{P_{\max }} = \frac{{E_{g,eff}^2}}{{4{R_G}}}\)