We consider an electromagnetic monochromatic progressive plane wave (HPPW) of angular frequency \(\omega\) propagating in a vacuum.

We chose (Oz) axis as the axis of propagation, \(\vec k=\omega/c \;\vec u_z\) is the wave vector of the HPPW.

In complex notation, the electric field of the wave is :

\(\underline {\vec E} = {\underline {\vec E} _0}\;{e^{i(\omega t - kz)}}\)

We denote :

\({\underline {\vec E} _0} = {E_{0x}}{e^{ - i{\varphi _x}}}{\vec u_x} + {E_{0y}}{e^{ - i{\varphi _y}}}{\vec u_y}\)

Where \(E_{0x}\) and \(E_{0y}\) are positive constants (with a good choice of phases \(\varphi_x\) and \(\varphi_y\)).

Furthermore, by careful selection of the origin of time, we will choose \(\varphi_x=0\) and we note \(\varphi=\varphi_y\) the phase shift of \(E_y\) compared to \(E_x\).

So, in real notation :

\(\begin{array}{l}{E_x} = {E_{0x}}\cos (\omega t - kz) \\{E_y} = {E_{0y}}\cos (\omega t - kz - \varphi ) \\\end{array}\)

The magnetic field is deduced (from \(\vec B = \frac{{{{\vec u}_z} \wedge \vec E}}{c}\)) :

\(\begin{array}{l}{B_x} = - \frac{{{E_{0y}}}}{c}\cos (\omega t - kz) \\{B_y} = \frac{{{E_{0x}}}}{c}\cos (\omega t - kz - \varphi ) \\\end{array}\)

The polarization of an electromagnetic wave is given by the behavior of its electric field.

More specifically, the polarization of a wave is characterized by the trajectory of the extremity of the electrical field of the wave in a wave plane.

To define the polarization of a harmonic progressive electromagnetic plane wave, we always place in a given \(z=z_0\), that the null value will be taken for example.

Therefore, the coordinates of electric field become :

\(\begin{array}{l}{E_x} = {E_{0x}}\cos (\omega t) \\{E_y} = {E_{0y}}\cos (\omega t - \varphi ) \\\end{array}\)

• Linear polarization :

  Linear polarization corresponds to the case when the electric field has a constant direction over time that can be chosen parallel to the axis (Ox) :

  \(\vec E = {E_0}\cos \omega t\;{\vec u_x}\)

  To an observer in a plane of fixed high, the field oscillates as a function of time along the (Ox) axis.

• Circular polarization :

  If \(\varphi=\pm \pi/2\) , the coordinates \(E_x\) and \(E_y\) of the electric field are in quadrature : the axes of the ellipse representing the trajectory of the extremity of the vector \(\vec E\) coincide with the axes (Ox) and (Oy).

  If \(\varphi=+\pi/2\) :

  \({E_x} = {E_{0x}}\cos (\omega t)\;\;\;\;and\;\;\;\;{E_y} = {E_{0y}}\sin (\omega t)\)

  So :

  \({\left( {\frac{{{E_x}}}{{{E_{0x}}}}} \right)^2} + {\left( {\frac{{{E_y}}}{{{E_{0y}}}}} \right)^2} = 1\)

  This is the equation of an ellipse axis (Ox) and (Oy), of lengths \(E_{0x}\) and \(E_{0y}\).

  If the amplitudes \(E_{0x}\) and \(E_{0y}\) are identically equal to \(E_0\), the ellipse corresponds to a circle :

  \(E_x^2 + E_y^2 = E_0^2\)

  The polarization of the electromagnetic wave is called circular.

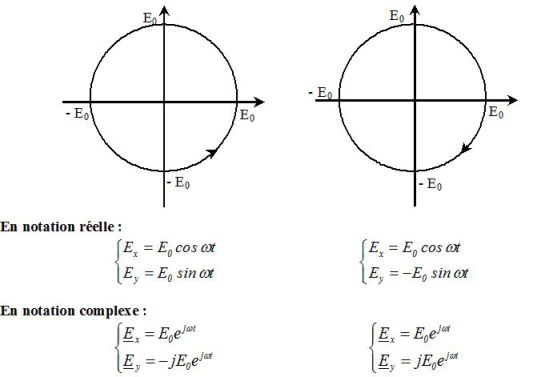
  It is easily shown that if \(\varphi=+\pi/2\), the wave is left circular and that if \(\varphi=-\pi/2\), the wave is right circular.

  The following figure shows on the left, the left circular polarization corresponding to \(\varphi=+\pi/2\) and on the right, the right circular polarization corresponding to \(\varphi=-\pi/2\).

• Elliptical polarization :

  Remember that :

  \(\begin{array}{l}{E_x} = {E_{0x}}\cos (\omega t) \\{E_y} = {E_{0y}}\cos (\omega t - \varphi ) \\\end{array}\)

  Coordinate along (Oy) can also be written :

  \({E_y} = {E_{0y}}(\cos \omega t\cos \varphi + \sin \omega t\sin \varphi )\)

  To eliminate the time, we write that :

  \(\cos (\omega t) = \frac{{{E_x}}}{{{E_{0x}}}}\)

  \(\sin \omega t = \frac{1}{{\sin \varphi }}\left( {\frac{{{E_y}}}{{{E_{0y}}}} - \frac{{{E_x}}}{{{E_{0x}}}}\cos \varphi } \right)\)

  Therefore, using \({\cos ^2}\omega t + {\sin ^2}\omega t = 1\) :

  \({\left( {\frac{{{E_x}}}{{{E_{0x}}}}} \right)^2} + \frac{1}{{{{\sin }^2}\varphi }}\left( {{{\left( {\frac{{{E_y}}}{{{E_{0y}}}}} \right)}^2} - 2\left( {\frac{{{E_y}}}{{{E_{0y}}}}} \right)\left( {\frac{{{E_x}}}{{{E_{0x}}}}} \right)\cos \varphi + {{\left( {\frac{{{E_x}}}{{{E_{0x}}}}} \right)}^2}{{\cos }^2}\varphi } \right) = 1\)

  So :

  \({\left( {\frac{{{E_x}}}{{{E_{0x}}}}} \right)^2} - 2\left( {\frac{{{E_x}}}{{{E_{0x}}}}} \right)\left( {\frac{{{E_y}}}{{{E_{0y}}}}} \right)\cos \varphi + {\left( {\frac{{{E_y}}}{{{E_{0y}}}}} \right)^2} = {\sin ^2}\varphi\)

  This is the equation of an ellipse in Cartesian coordinates.

In the case of natural light :

For most classical light sources, the emitted light corresponds to the superposition of a MPPW in a very short time (of the order of \(10^{-10}s\), but do not forget that the period of these waves is of the order of \(10^{-15}s\)) and polarization well fixed for each wave but changing randomly between two monochromatic progressive plane waves.

The optical sensors are sensitive to the average value over time of the square of the electric field (this is the light intensity) over the periods of the order of \(10^{-12}s\) (eye) to \(10^{-6}s\) (good photoelectric cell).

They therefore can not follow the polarization of one of MPPW whose successive forms of the visible light : it is said that natural light is not polarized.