Scalar theory of light, light intensity (illumination)
Fondamental : Light intensity (or illumination)
The wave optics calculations typically involve determining the intensity resulting from the superposition of several waves.
To calculate the intensity, it is often possible to forget the vector character of the electric field : the scalar theory of light.
In many situations, the light intensity, due to the superposition of several electromagnetic waves can be determined by means of a simplified model, where the electric field is associated with a scalar magnitude.
This approximation is justified :
In the very common case of non-polarized waves whose propagation directions are similar.
Polarized waves known that the polarization directions are similar.
Conventional sensors are called "quadratic" : they are sensitive to the time average value (on the times which is longer than the period of the light waves which is of the order of some \(10^{-15}s\)) of the square of the electric fields module.
We note \(s(M,t)\) the amplitude of the electric field (and \(\underline s\) in complex notation).
We define the quantity "light intensity" or "Illumination" by :
\(I = k{\left\langle {s{{(M,t)}^2}} \right\rangle _t} = \frac{1}{2}k\;{\mathop{\rm Re}\nolimits} (\underline s .{\underline s ^*}) = \frac{1}{2}k{\left| {\underline s } \right|^2}\)
Where \(k\) is a multiplicative constant.
The illumination is expressed in \(W.m^{-2}\) and is connected to the module of the Poynting vector.
We have seen in fact that, for a harmonic progressive plane wave, this vector was written :
\(\vec \Pi = {\varepsilon _0}c\;{\vec E^2}\;{\vec u_z}\)
and was well proportional to the square of the electric field.
Fondamental : Composition of two light vibrations
Considering the composition of two light waves \(\underline {\vec s}_1\) and \(\underline {\vec s}_2\) and propagating in directions quasi-parallel of the unit vector \(\vec u_z\).
These vectors are perpendicular to \(\vec u_z\), are projected on axes (Ox) and (Oy) forming with (Oz) a direct basis :
\({\underline {\vec s} _1} + {\underline {\vec s}_2} = (\underline {{s}}_{1,x} + \underline {{s}}_{2,x} )\;{\vec u_x} + (\underline {{s}}_{1,y} + \underline {{s}}_{2,y} )\;{\vec u_y}\)
The total light intensity is :
\(I = \frac{1}{2}k{\left| {{{\underline {\vec s} }_1} + {{\underline {\vec s} }_2}} \right|^2} = \frac{1}{2}k\left( {{{({{\underline s }_{1,x}} + {{\underline s }_{2,x}})}^2} + {{({{\underline s }_{1,y}} + {{\underline s }_{2,y}})}^2}} \right)\)
The total illumination is the sum of the illuminations for the two projection directions ; we can just study the composition of two light vibrations of the same linear polarization.
With a suitable choice of the origin of time and by harmonic analysis of the problem, we can write :
\({\underline s _1}(M,t) = {A_1}{e^{i\omega t}}\;\;\;\;\;;\;\;\;\;\;{\underline s _2}(M,t) = {A_2}{e^{i(\omega t - \varphi (M,t))}}\)
The resulting wave is :
\(\underline s (M,t) = {\underline s _1}(M,t) + {\underline s _2}(M,t) = ({A_1} + {A_2}{e^{ - i\varphi (M,t))}}){e^{i\omega t}}\)
Fondamental : Resulting Intensity (Fresnel formula)
Two synchronous waves are considered (same frequency and a phase shift which is independent of time).
Moreover, the two waves have the same amplitude :
\(\underline s (M,t) =A_0 (1 +e^{ - i\varphi (M)}){e^{i\omega t}}\)
The light intensity calculated according to :
\(I(M)=\frac {1}{2}k\;Re(\underline s(M,t) \underline s^*(M,t))=\frac {1}{2} k\; {\left| {\underline s (M,t)} \right|^2}\)
Is :
\(I(M)=\frac {1}{2}k A_0^2 (1 +e^{ - i\varphi (M)})(1 +e^{ + i\varphi (M)})\)
Finally, by denoting \(I_0=\frac{1}{2}kA_0^2\) :
\(I(M)=2I_0 (1+cos(\varphi(M))\)
This is the Fresnel formula for the light intensity at the interference between two synchronous waves.
Recall that the phase shift at the point \(M\) is connected to the optical path difference \(\delta (M)\) by the relationship :
\(\varphi (M) = \frac {2\pi}{\lambda_0}\delta (M)\)
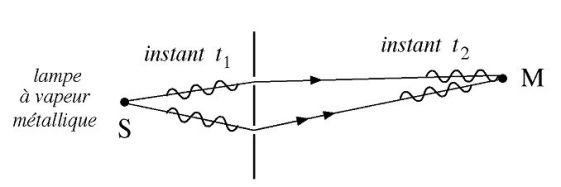
Fondamental : Temporal coherence
Is limited to a point source \((S)\) which emits wave trains of average duration \(\tau_c\), that occupy space in a length (coherence length) equal to :
\(L_c=c \tau_c\)
Each wave train from \((S)\) is divided into two wave trains and has, at a point \(M\), time delay :
\(\Delta t = \frac{{{{(SM)}_2}}}{c} - \frac{{{{(SM)}_1}}}{c} = \frac{{\delta (M)}}{c}\)
If \(\Delta t << \tau_c\) (either \(\delta (M)<<L_c\)) :
The two wave trains interfere in \(M\) are from the same wave train emitted by \((S)\).
The phase shift between the two waves is constant, the two waves are coherent and observed interference.
To have an interference, the waves from \(S_1\) and from \(S_2\) come from the de-excitation of the same atom.
Then the random phase variations over time affect \(S_1\) and \(S_2\) the same way and the phase difference \(\varphi (M)\) is then constant in time.
\(S_1\) and \(S_2\) must be images from a single source \(S\) (often by means of material of a geometric optics), the waves simply go through different optical paths but are issued by the same point \(S\).
It is said as well as secondary sources \(S_1\) and \(S_2\) are coherent between each other.
Fondamental : Spatial Coherence
Is considered a "broad" source, consisting of a ensemble of incoherent point sources between each other, spread over a surface or in a volume.
The sources are incoherent with each other, the intensities will have to add : if the source is wide, the interference will no longer be observed.
However, if the source is "bit extended", interference fringes can be observed but with a weakened contrast.
The length of spatial coherence \(L_S\) is the maximum width of the source giving an interference pattern bit blurred.