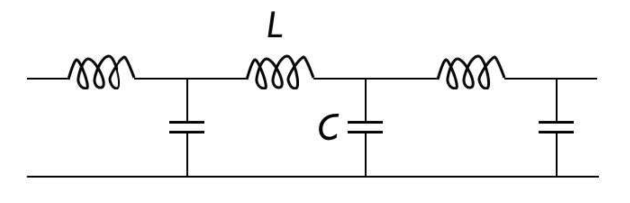
Transmission along an LC network
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
Question
Determine the dispersion relation for a periodic wave crossing the line.
What is the cutoff frequency ?
Indice
Write Kirchhoff's laws.
One can also use the Millman's theorem.
Solution
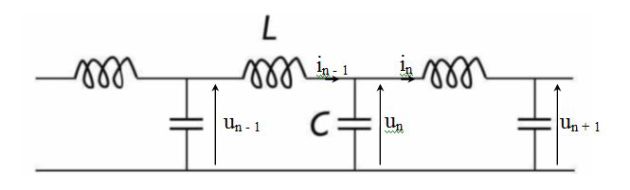
Is \(u_n(t)\) the voltage across capacitor \(C\) of the cell number \(n\) and \(i_n(t)\) the current in the coil follows (see figure), we can write :
\(u_{n-1}(t)=u_{n}(t)+L\frac{di_{n-1}(t)}{dt}\;\;\;\;and\;\;\;\;u_n(t)=u_{n+1}(t)+L\frac{di_n(t)}{dt}\)
\(i_{n-1}(t)=i_{n}(t)+C\frac{du_{n}(t)}{dt}\)
The last equation is derived with respect to time :
\(\frac {di_{n-1}(t)}{dt}=\frac{di_{n}(t)}{dt}+C\frac{d^2u_{n}(t)}{dt^2}\)
And used two loop laws :
\(\frac{u_{n-1}(t)-u_n(t)}{L}=\frac{u_{n}(t)-u_{n+1}(t)}{L}+C\frac{d^2u_{n}(t)}{dt^2}\)
Whence :
\(LC\frac{d^2u_{n}(t)}{dt^2}=u_{n-1}(t)+u_{n+1}(t)-2u_{n}(t)\)
We are interested in the propagation of plane waves that we write in the form :
\(u_n(t)=A\;exp(i(\omega t - kna))\)
where \(a\) is the "width" of a cell.
The previous differential equation then becomes :
\(-LC\omega^2=e^{-ika}+e^{ika}-2=2cos(ka)-2\)
Or, finally :
\(\omega=\frac{2}{\sqrt{LC}}sin(\frac{ka}{2})\)
It is requested dispersion relation.
The cut-off frequency is obtained when \(sin(ka/2)\) is equal to \(1\) :
\(\omega_c=\frac{2}{\sqrt{LC}}\)
Question
Determine the propagation equation satisfied by the voltage across the capacitors within the approximation of continuous medium.
Solution
It is assumed that the distance between the cells \(a\) is small compared to the wavelength (\(a<<\lambda)\).
We can then define a function \(u(x,t)\) such as (Taylor-Young Development of the second order) :
\(\left\{ \begin{array}{l}u_{n + 1} (t) = u((n+1)a ,t) = u(na ,t) + \frac{{\partial u}}{{\partial x}}a + \frac{1}{2}\frac{{\partial ^2 u}}{{\partial x^2 }}a^2 \\u_{n - 1} (t) = u((n-1)a,t)=u(na ,t) - \frac{{\partial u}}{{\partial x}}a + \frac{1}{2}\frac{{\partial ^2 u}}{{\partial x^2 }}a^2 \\\end{array} \right.\)
And the propagation equation becomes :
\(LC\frac{{\partial ^2 u(x,t)}}{{\partial t^2 }} = \frac{{\partial ^2 u(x,t)}}{{\partial x^2 }}\;a^2 \)
Is :
\(\frac{{\partial ^2 u(x,t)}}{{\partial x^2 }} - \frac{1}{{c^2 }}\frac{{\partial ^2 u(x,t)}}{{\partial t^2 }} = 0\;\;\;\;\;\;\;\;\;\;with\;\;\;\;\;\;\;\;\;\;c = \frac{{a }}{\sqrt{LC}}\)
We find a d'Alembert equation, characteristic of a propagation without dissipation at the speed \(c\).
Complément :
We take the dispersion relation obtained in the first question :
\(\omega=\frac{2}{\sqrt{LC}}sin(\frac{ka}{2})\)
And assume that \(a<<\lambda\) (assumption of continuous medium).
So :
\(ka=\frac{2\pi}{\lambda}a<<1\)
Consequently :
\(\omega=\frac{2}{\sqrt{LC}}sin(\frac{ka}{2})\approx \frac{2}{\sqrt{LC}}(\frac{ka}{2})=\frac{a}{\sqrt{LC}}k\)
The phase velocity (equal here also to the group velocity) is then :
\(v_{\varphi}=\frac{\omega}{k}= \frac{{a }}{\sqrt{LC}}\)
We find the speed of the wave obtained in the second question.