Reflection and transmission of sound waves
Fondamental : Boundary condition across a sound diopter
We study the reflection and transmission of a wave at normal incidence.
Medium \((1)\) and \((2)\) have different physical characteristics a priori but the pressure at equilibrium is identical, denoted \(P_0\).
A surface which delimits two different media is called "acoustic diopter".
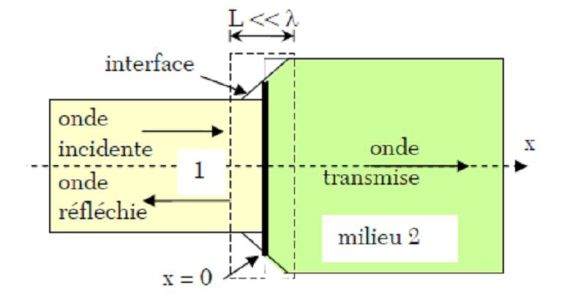
We study the reflection and transmission of plane sound waves at the connection of two pipe of cross sections \(S_1\) and \(S_2\), separated between two materials of acoustic impedances \(z_1\) for \(x<0\) and \(z_2\) for \(x>0\).
Recall that the acoustic impedance is defined from :
\(z = \frac {p}{v}\)
We note :
\(z_1=\mu_1c_1\;\;\;\;\;and\;\;\;\;\;z_2=\mu_2c_2\)
Continuity of the volume flow rate at the interface :
It is considered that the two fluids do not mix, so that the interface is an impermeable membrane.
\(V\) is a volume in the connection area between the two cross sections \(\Sigma_1\) and \(\Sigma_2\), located in \(x=-\varepsilon\) and \(x=+\varepsilon\).
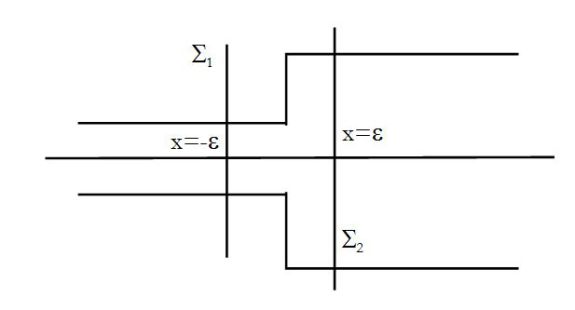
One can imagine the volume (\(V\)) which oscillates to both sides of the separation membrane and directly write the conservation of volume, resulting in the conservation of volume flow rate :
\({v_1}{S_1} = {v_2}{S_2}\)
In the particular case where the two cross sections are equal, then there is continuity of the speed of both sides of the membrane.
Continuity of pressure :
In the acoustic approximation, the displacement of the interface is small compared to the wavelength and can be neglected, so that the interface is confused with the plane \(x=0\).
It is assumed that the pressure at rest \(P_0\) has the same value at any point in space.
Considering a surface element \(dS\) of the interface between the two fluids as a fictitious massless membrane, is shown with the Newton's second law in projection on the \((Ox)\) axis that pressure is continuous at the interface.
Indeed :
\(({P_0} + {p_1}(x=0^-,t))dS - ({P_0} + {p_2}(x=0^+,t))dS = 0\;\;\;\;\;so\;\;\;\;\;{p_1}(x=0^-,t) = {p_2}(x=0^+,t)\)
Remark :
In case the interface is treated as a flat plate of mass surface density \(\sigma\), relationship between the pressures on either side of the interface can now be written :
\(\sigma \frac {\partial v}{\partial t} (0,t)=p_1(x=0^-,t)-p_2(x=0^+,t)\)
Fondamental : Coefficients of reflection and transmission in amplitude
It is assumed that the two cross sections are identical :
\(S_1=S_2\)
It is considered that the incident wave is a HPPW :
\(\underline v_i(x,t)=\underline A_i \;exp(j(\omega t - k_1x))\)
The reflected and transmitted waves are noted :
\(\underline v_r(x,t)=\underline A_r \;exp(j(\omega t + k_1x))\)
And :
\(\underline v_t(x,t)=\underline A_t \;exp(j(\omega t - k_2x))\)
The wave vectors are given by :
\(k_1=\frac{\omega}{c_1}\)
And :
\(k_2=\frac{\omega}{c_2}\)
Where \(c_1\) and \(c_2\) are the sound velocities in the two medium.
Overpressure are deduced using the relationship \(\underline p=\pm\mu c \;\underline v=\pm z\;\underline v\), so :
\(\underline p_i(x,t)=z_1\underline A_i \;exp(j(\omega t - k_1x))\)
\(\underline p_r(x,t)=-z_1\underline A_r \;exp(j(\omega t + k_1x))\)
\(\underline p_t(x,t)=z_2\underline A_t \;exp(j(\omega t - k_2x))\)
Using the boundary condition :
Continuity of the volume flow rate at the interface \(x=0\) (continuity of speed since the cross sections are the same) :
\(\underline A_i+\underline A_r= \underline A_t\)
Continuity of overpressure at the interface \(x=0\) :
\(z_1(\underline A_i-\underline A_r)=z_2 \underline A_t\)
Expression of the coefficients of reflection and transmission in amplitude :
The previous system is solved as :
\(\underline r_v=\frac{\underline A_r}{\underline A_i}=\frac{z_1-z_2}{z_1+z_2}\)
And :
\(\underline t_v=\frac{\underline A_t}{\underline A_i}=\frac{2z_1}{z_1+z_2}\)
\(\underline r_v\) is the reflection coefficient in amplitude for speed and \(\underline t_v\) is that for the transmission for speed also.
The coefficients of reflection and transmission to the pressure are deduced :
\(\underline r_p=-\frac{\underline A_r}{\underline A_i}=\frac{z_2-z_1}{z_1+z_2}=-\underline r_v\)
And :
\(\underline t_p=\frac{\mu_2c_2}{\mu_1c_1}\;\frac{\underline A_t}{\underline A_i}=\frac{2z_2}{z_1+z_2}\)
Some notes :
The transmission coefficients (\(\underline t_v\) and \(\underline t_p\)) are real positives : the transmitted wave is always in phase with the incident wave.
The reflection coefficients may be positive or negative : the reflected wave can be in phase or in phase opposition with the incident wave.
When \(z_1=z_2\), there is no reflected wave (called adaptation of impedance).
The sound wave in the medium \((1)\) results from the superposition of two HPPW propagating in opposite direction and whose amplitudes generally differ.
It is not either of a traveling wave or a standing wave but a wave having a SWR (standing wave ratio).
In the special case \(z_2>>z_1\) :
\(r_v\approx-1\;\;\;\;\; ;\;\;\;\;\;r_p\approx1\;\;\;\;\; ;\;\;\;\;\;t_v\approx0\;\;\;\;\; ;\;\;\;\;\;t_p\approx2\)
There is no more transmitted wave. Standing waves is shown that is obtained in the medium \((1)\) with speed node and pressure anti-node in \(x=0\).
This is the case of an air interface to solid.
If \(z_2<<z_1\), so :
\(r_v\approx1\;\;\;\;\; ;\;\;\;\;\;r_p\approx -1\;\;\;\;\; ;\;\;\;\;\;t_v\approx 2\;\;\;\;\; ;\;\;\;\;\;t_p\approx 0\)
There is no more transmitted wave. Standing wave is always obtained in the medium \((1)\), but with a speed anti-node and pressure node in \(x=0\).
This is the case of a solid-to-air interface.
Fondamental : Coefficients of reflection and transmission in energy
On average, the "surface density of sound power" vectors of the three incident, reflected and transmitted waves are :
\(\left\langle {{\Pi _i}} \right\rangle = \frac{1}{2}{z_1}A_i^2\;\;\;\;\;;\;\;\;\;\;\left\langle {{\Pi _i}} \right\rangle = \frac{1}{2}{z_1}A_r^2\,\,\,\,\,;\,\,\,\,\,\left\langle {{\Pi _i}} \right\rangle = \frac{1}{2}{z_2}A_t^2\)
We deduce the coefficients of reflection and transmission in energy :
\(R = \frac{{\left\langle {{\Pi _r}} \right\rangle }}{{\left\langle {{\Pi _i}} \right\rangle }} = r_v^2 = {\left( {\frac{{{z_1} - {z_2}}}{{{z_1} + {z_2}}}} \right)^2}\;\;\;\;\;and\;\;\;\;\;T = \frac{{\left\langle {{\Pi _t}} \right\rangle }}{{\left\langle {{\Pi _i}} \right\rangle }} = \frac{{4{z_1}{z_2}}}{{{{({z_1} + {z_2})}^2}}}\)
Remarks :
Energy conservation :
\(R+T=1\)
When \(z_1>>z_2\) or \(z_2>>z_1\), \(R\approx 1\) and \(T\approx 0\) : there is no transmitted wave.
For \(z_1\) data, the coefficient \(T\) is maximum when \(z_2=z_1\) : there is the adaptation of impedance.
An interface correctly transmits sound waves only if the impedances of both sides are almost equal.
Complément : Musical instruments (trumpets, organ pipes, ...)
Complément : A little music : stationary sound waves
In the case of an acoustic diopter between two identical mediums, but with different cross sections \(S_1\) and \(S_2\), one leads to the coefficients of reflection and transmission in amplitude for the following speed and the pressure :
\(t_v=\frac{2}{1+S_2/S_1}\;\;\;\; ;\;\;\;\;r_v=\frac{S_2/S_1-1}{S_2/S_1+1}\;\;\;\; ;\;\;\;\;t_p=t_v\;\;\;\; ;\;\;\;\;r_p=-r_v\)
We deduce that :
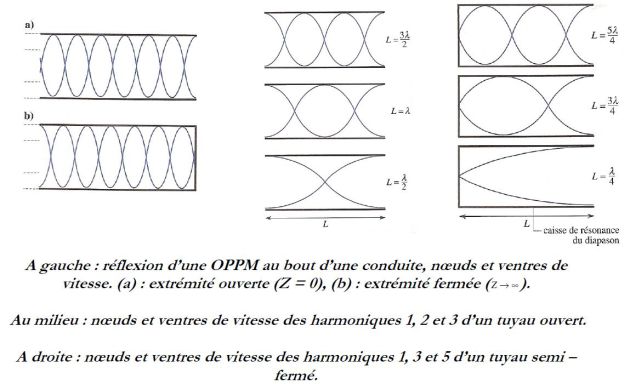
For a pipe (organ, for example) open at one end (then \(S_2>>S_1\)) :
There is a pressure node and a speed anti-node at the end.
For a pipe closed at one end (\(S_2<<S_1\)) :
There is a speed node and an overpressure anti-node at the end.
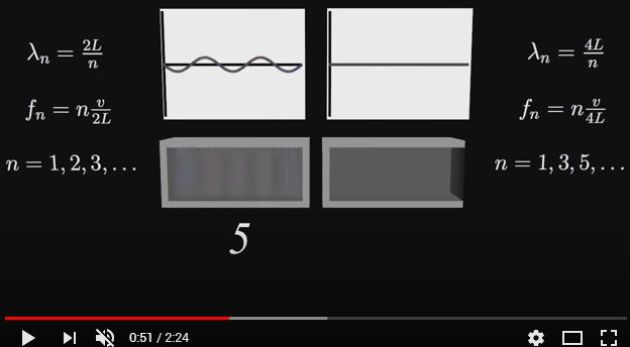
Frequencies in a sound pipe :
The pipe ends are of the same nature :
The pipe length must be an integer multiple of the distance between two nodes (or two antinodes) or an integer multiple of the half wavelength.
The frequency of the fundamental mode is then \(\nu_1=c/2L\), where \(L\) is the length of the pipe and \(c\) the speed of sound.
The frequencies of the different harmonics are the even and odd multiples of the fundamental.
The pipe ends are different in nature :
The length of the hose must be an integer multiple of the \(\lambda\) increased of \(\lambda/4\).
The frequency of the fundamental mode is then \(\nu_1=c/4L\), where \(L\) is the length of the pipe and \(c\) the speed of sound.
The frequencies of the different harmonics are the only odd multiples of the fundamental.