L'effet Hall
Fondamental : Action d'un champ magnétique sur le mouvement des porteurs de charges
Dans un conducteur métallique (« ohmique ») soumis à une tension électrique, les électrons de conduction se mettent en mouvement.
La fiche de cours sur la loi d'Ohm locale a précisé les notations.
Le conducteur ohmique est de plus placé dans un champ magnétique \(\vec B\).
Le PFD appliqué à un porteur de charge devient :
\(m\frac{{d\vec v}}{{dt}} = q(\vec E + \vec v \wedge \vec B) - k\vec v\;\;\;\;\;soit\;\;\;\;\;\frac{{d\vec v}}{{dt}} + \frac{1}{\tau }\vec v = \frac{q}{m}(\vec E + \vec v \wedge \vec B)\)
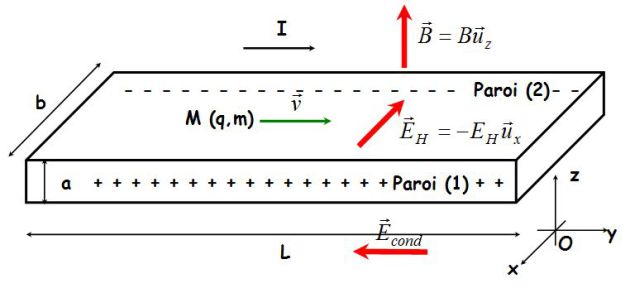
La figure suivante précise la géométrie du conducteur utilisé : c'est une plaquette parallélépipédique, de longueur \(L\).
Le champ magnétique extérieur est \(\vec B = B \vec u_z\).
Le champ électrique créé par le générateur et mettant en mouvement les porteurs de charge est noté \(\vec E_e\).
En régime permanent, les électrons se déplacent à la vitesse \(\vec v = v \vec u_y\).
En régime permanent (\(t>>\tau\)) :
\(\vec v = \frac{{\tau q}}{m}(\vec E + \vec v \wedge \vec B)\)
Le terme magnétique \(q \vec v \wedge \vec B\) est dirigé selon Ox. Il apparaît donc un champ électrique, dit champ de Hall \(\vec E_H\) tel que :
\(\vec E=\vec E_e+\vec E_H\)
Avec :
\(\vec E_H+\vec v \wedge \vec B = \vec 0\)
Ainsi, la vitesse des porteurs devient :
\(\vec v = \frac{{\tau q}}{m}\vec E_e\)
Ce champ de Hall est dû aux déplacements d'électrons pendant un bref instant (durée du régime transitoire) vers la paroi (2), créant ainsi une dissymétrie de charges et donc un champ électrique dirigé de la paroi (1) vers la paroi (2).
Fondamental : Calcul de la tension Hall
Le champ électrique de Hall vaut :
\({\vec E_H} = - \vec v \wedge \vec B = - v\;{\vec u_y} \wedge B\;{\vec u_z} = - vB\;{\vec u_x}\)
La tension de Hall \(\Delta V_H\) s'obtient en exprimant la circulation de ce champ :
\(\int_0^{ - b} {{{\vec E}_H}.dx\;{{\vec u}_x}} = \int_0^{ - b} {( - vB\;{{\vec u}_x}).dx\;{{\vec u}_x}} = vbB = - ({V_2} - {V_1}) = {V_1} - {V_2} = \Delta {V_H}\)
Ainsi :
\(\Delta {V_H} = vbB\)
L'intensité du courant est :
\(I = jab = nqvab\)
Ainsi :
\(\Delta {V_H} = \frac{I}{{nqab}}bB = \frac{1}{{nq}}\frac{{IB}}{a}\)
Si \(q=-e\) (cas d'électrons de conduction, avec \(I<0\) sur la figure) :
\(\Delta {V_H} = - \frac{1}{{ne}}\frac{{IB}}{a} = - {R_H}\frac{{IB}}{a}\;\;\;\;\;\;(avec\;{R_H} = \frac{1}{{ne}},\;constante\;de\;Hall)\)
On voit ainsi que la tension de Hall est proportionnelle au champ magnétique appliqué.
Les sondes à effet Hall permettent de mesurer cette tension et d'en déduire ensuite le champ magnétique.
Complément : La force de Laplace
Voir la suite dans la fiche de cours consacrée à la force de Laplace.