Force de Laplace
Fondamental : Cas d'un conducteur parallélépipédique
Cette fiche de cours reprend les notations de la fiche de cours sur l'effet Hall.
La vidéo suivante met en évidence expérimentalement la force de Laplace.
On veut exprimer la force subie par le conducteur dans un champ magnétique \(\vec B\).
L'ensemble du conducteur (électrons de conduction et cations métalliques) est soumis, de la part du champ magnétique \(\vec B\) aux forces :
Sur les électrons de conduction :
\(n(abL)\;\left[ { -e\vec E_e - e{{\vec E}_H} + - e\vec v \wedge \vec B} \right]\)
où \(n\) est la densité de porteurs de charges.
Sur les cations métalliques (immobiles) :
\(n(abL)\;\left[ {e\vec E_e +e{{\vec E}_H}} \right]\)
Globalement, le conducteur est donc soumis à la force :
\({\vec F_L} = n(abL)\;\left[ { - e\vec v \wedge \vec B} \right]\)
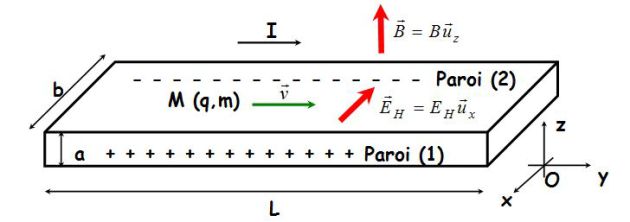
L'intensité I s'exprime sous la forme :
\(I = jab = - nevab\)
D'où :
\({\vec F_L} = IL\;{\vec u_y} \wedge \vec B = I\;\vec L \wedge \vec B\)
Attention : Force de Laplace pour un conducteur filiforme
On considère un tronçon de circuit filiforme parcouru par un courant d'intensité I et plongé dans un champ magnétique \(\vec B\) quelconque.
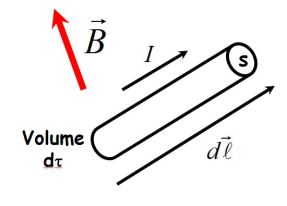
Le conducteur est soumis à la force (appelée force de Laplace) :
\(d{\vec F_L} = I\;d\vec \ell \wedge \vec B\)
En notant que :
\(I = js\;\;\;soit\;\;\;I\;d\vec \ell = js\;d\vec \ell = \vec j\;s\;d\ell = \vec j\;d\tau\)
Alors :
\(d{\vec F_L} = \vec j\;d\tau \wedge \vec B\)
C'est l'expression de la force de Laplace pour des courants volumiques.
Différences entre force de Laplace et force de Lorentz :
La force de Lorentz est une force microscopique qui s'applique à des porteurs de charge \(q\) en mouvement dans un champ magnétique :
\(\vec f = q(\vec v \wedge \vec B)\)
La force de Laplace est une force macroscopique qui s'applique à tout le conducteur, électrons et cations compris.
