Vecteur densité volumique et intensité
Rappel :
On considère un ensemble de particules de charge q, de densité particulaire n* et ayant un mouvement d'ensemble à la vitesse \(\vec v\).
On notera dans la suite :
\(\rho_m=n^*q\)
La densité de charges mobiles.
Comment définir l'intensité qui traverse une surface dS quelconque ?
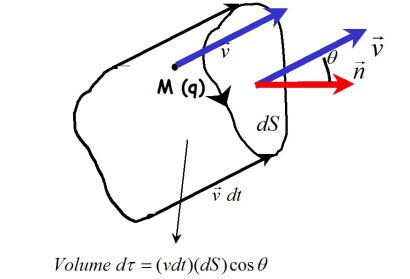
La quantité de charges électriques dq qui traverse la surface élémentaire dS pendant l'intervalle de temps dt est :
\(dq = n^* d\tau \;q = n^* (dS\cos \theta \;vdt)\;q\)
Or, \(vdScos\theta=\vec v.\vec ndS\), d'où :
\(dq = n^* (\vec v.\vec n\;dS)\;qdt = \vec j.\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over n} \;dS\;dt\)
Où l'on a défini :
\(\vec j = n^* q\;\vec v = \rho _m \vec v\)
Le vecteur densité de courant.
L'intensité \(di\) :
\(di = \frac{{dq}}{{dt}} = \vec j.\vec n\;dS\)
s'interprète comme le flux du vecteur densité de courant à travers la surface dS orientée.
L'intensité qui traverse une surface finie (S) sera alors :
\(i = \iint_S\vec j.\vec n\;dS\)
Attention : Définition de l'intensité
L'intensité d'un courant s'interprète comme le flux du vecteur densité de courant à travers la surface S orientée :
\(i = \iint_S\vec j.\vec n\;dS\)
Complément : Différences entre modélisation volumique et surfacique
Dans le cas d'une répartition volumique de courants :
\(\vec j = \rho \vec v\;\;\;\;\;;\;\;\;\;\;di = \vec j.\vec ndS\)
Pour une répartition surfacique :
\(\vec j = \sigma \vec v\;\;\;\;\;;\;\;\;\;\;di = \vec j.\vec nd\ell\)
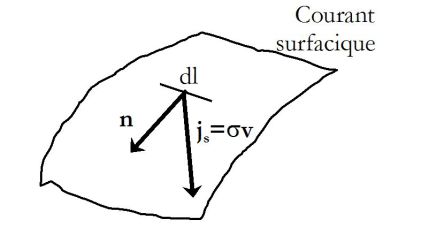
Au lieu de compter les charges qui traversent une surface donnée, on compte les charges qui traversent un segment de longueur \(d\ell\) et de vecteur normal \(\vec n\).