Bilans de quantités de mouvements et de moments cinétiques
Exemple : Force exercée sur un coude de canalisation
De l'eau de masse volumique \(\mu\) coule en régime stationnaire avec un débit massique \(D_m\) dans une canalisation horizontale de section constante S faisant un coude d'angle droit.
On néglige la pesanteur et l'écoulement est supposé parfait.
Loin du coude en amont, la pression est uniforme et vaut \(P_1\) et l'écoulement est unidimensionnel de vitesse \(v_1\vec u_x\).
Loin du coude en aval, la pression uniforme vaut \(P_2\) et la vitesse \(v_2\vec u_y\).
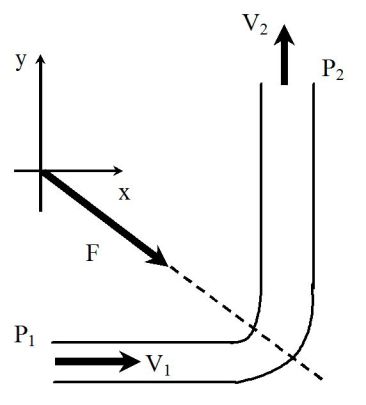
Calculs de \(v_2\) et de \(P_2\) :
La conservation du débit volumique conduit à \(v_1=v_2\).
Le théorème de Bernoulli (valable ici car l'écoulement est stationnaire, parfait, incompressible, homogène) donne (le tube est horizontal !) :
\(\frac{1}{2}\mu v_1^2 + P_1 = \frac{1}{2}\mu v_2^2 + P_2 \;\;\;\;\;\;\;\;\;\;soit\;\;\;\;\;\;\;\;\;\;P_1 = P_2 = P_0\)
Calcul de la force subie par la canalisation (bilan de quantité de mouvement) :
La force \(\vec F\) exercée par l'eau sur la canalisation est égale à l'opposée \(-\vec F\) de la force exercée par la canalisation sur l'eau.
En l'absence de viscosité, il s'agit aussi de la résultante des forces de pression sur la paroi latérale (T) de la canalisation.
Un bilan de quantité de mouvement sur l'eau contenue dans la canalisation permet de calculer cette force.
On raisonne sur le système fermé suivant : le contenu de tube coudé et la masse \(dm\) qui rentre en amont entre les instants \(t\) et \(t+dt\)..
La variation de quantité de mouvement de ce système vaut :
\(D\vec p = \left[ {\vec p(t + dt) + (\delta m )v_2 \vec u_y } \right] - \left[ {\vec p(t) + (\delta m)v_1 \vec u_x } \right]\)
Or : (on est en régime stationnaire)
\(\vec p(t + dt) = \vec p(t)\)
Et :
\(\delta m=\mu S vdt\)
Par conséquent :
\(\frac{{D\vec p}}{{Dt}} = \mu Sv^2 (\vec u_y - \vec u_x )\)
Le fluide est soumis aux forces :
le poids (négligé)
A la force \(-\vec F\)
Et aux forces de pression à l'entrée (\(P_0S\vec u_x0\)) et à la sortie (\(-P_0S\vec u_y\) ) du tube.
Le théorème de la résultante cinétique donne :
\(\frac{{D\vec p}}{{Dt}} = \mu Sv^2 (\vec u_y - \vec u_x ) = - \vec F + P_0 S(\vec u_x - \vec u_y )\)
On en déduit la force exercée par l'eau sur la canalisation :
\(\vec F = (P_0 S + \mu Sv^2 )(\vec u_x - \vec u_y )\)
La direction de la force était attendue ; cette force est la résultante des forces de pression exercées par l'eau sur la canalisation.
Sa direction et son sens montrent qu'au voisinage du coude, il existe une surpression sur le bord extérieur de la canalisation par rapport au bord intérieur
Exemple : Poussée d'une fusée
On considère une fusée dont la masse à l'instant \(t\) est notée \(m(t)\).
Des gaz sont éjectés à la vitesse \(u\) par rapport à la fusée, avec un débit massique \(D_m\).
On note \(m_0\) la masse initiale de la fusée (comprenant celle des gaz initiale).
On définit le système fermé suivant :
A l'instant \(t\) : la fusée de masse \(m(t)\) et de vitesse \(v(t)\), donc de quantité de mouvement :
\(p(t)=m(t)v(t)\)
A l'instant \(t+dt\) : la fusée de masse \(m(t)+dm\) (avec \(dm<0\)), de vitesse \(v(t)+dv\) et le sable de masse \((-dm)\) et de vitesse, par rapport au sol, \(v(t)-u\).
La quantité de mouvement de ce système est alors : (au 1er ordre)
\(p(t+dt)=(m(t)+dm)(v(t)+dv)+(-dm)(v(t)-u) \approx m(t)v(t)+m(t)dv+dm\;u\)
La variation de quantité de mouvement de ce système est alors :
\(Dp=p(t+dt)-p(t) = m(t)dv+dm\;u\)
Le théorème de la résultante cinétique donne alors : (en remarquant que \(D_m=-dm/dt\))
\(\frac {Dp}{dt}= m(t)\frac{dv}{dt}-D_m\;u=-m(t)g\)
Soit :
\( m(t)\frac{dv}{dt}=D_m\;u-m(t)g\)
Le terme \(D_mu\) apparaît comme une force supplémentaire qui s'exerce sur le système ouvert "La fusée". C'est la force de poussée.
La masse de la fusée vaut :
\(m(t)=m_0-D_mt\)
Par conséquent :
\(dv(t)=\frac {D_mu}{m_0-D_mt}dt-gdt\)
Soit :
\(v(t) = u\ln \left( {\frac{{m_0 }}{{m_0 - D_m t}}} \right) - gt\)
Exemple : Vidéo : "Propulsion à l'aide d'un extincteur"
Exemple : Le tourniquet hydraulique
Un tourniquet est constitué de deux bras de longueur \(a\) et d'extrémité recourbée.
L'eau arrive par un conduit central avec un débit massique \(D_m\) et est éjectée avec une vitesse relative \(u\) par rapport au tourniquet dont la vitesse de rotation par rapport à son axe est \(\omega\).
On suppose que le tourniquet est initialement immobile.
Le système fermé est ici :
A l'instant \(t\) : le tourniquet et l'eau à l'intérieur plus la masse d'eau \(dm=D_mdt\) qui rentre entre \(t\) et \(t+dt\).
Le moment cinétique (par rapport à l'axe de rotation \(\Delta\)) de ce système est simplement :
\(L_{\Delta}(t)=J_{\Delta}\omega(t)\)
Où \(J_{\Delta}\) est le moment d'inertie du tourniquet par rapport à l'axe.
A l'instant \(t+dt\) : le tourniquet et l'eau à l'intérieur plus la même masse \(dm=D_mdt\) qui est éjectée au niveau des extrémités des bras du tourniquet.
Le moment cinétique du tourniquet devient \(L_{\Delta}(t+dt)=J_{\Delta}\omega(t+dt)\).
Le moment cinétique de l'eau éjectée par les buses est :
\(L_{buse,\Delta}=-D_mdt a (u-a\omega)\)
On a utilisé le fait que la vitesse d'éjection de l'eau, dans le référentiel du sol, était \(u-a\omega\).
La variation de moment cinétique est ainsi :
\(\frac {dL_{\Delta}}{dt}=J_{\Delta}\frac{d\omega}{dt}-D_ma(u-a\omega)\)
En l'absence de moment extérieur (pas de frottements), le théorème du moment cinétique donne :
\(J_{\Delta}\frac{d\omega}{dt}-D_ma(u-a\omega)=0\)
Soit :
\(\frac{d\omega}{dt}+\frac{D_ma^2}{J_{\Delta}}\omega=\frac{D_ma u}{J_{\Delta}}\)
Dont la solution est :
\(\omega (t) = \frac{u}{a}\left( {1 - e^{ - t/\tau } } \right)\;\;\;\;\;avec\;\;\;\;\;\tau = \frac{{J_\Delta }}{{D_m a^2 }}\)


