Inductance mutuelle
Consacrer 10 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
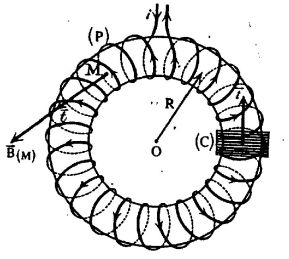
Sur un tore engendré par la rotation d'un cercle de rayon a sont bobinées régulièrement N spires parcourues par un courant i.
Sur cet enroulement (P) est constituée une bobine (C) comportant n spires de rayon a.
Question
Calculer le coefficient d'inductance mutuelle M des deux enroulements (P) et (C).
Indice
Comment définir M ? Quel est le champ le plus facile à calculer ?
Solution
On calcule le flux envoyé par le champ magnétique créé par le tore sur la bobine :
\(\phi = Mi\)
Où i est le courant qui circule dans le tore.
Le théorème d'Ampère permet de déterminer le champ créé par le tore à l'intérieur (il est nul à l'extérieur) :
\(\vec B = \frac{{\mu Ni}}{{2\pi }}\frac{1}{r}\vec u_\theta\)
On suppose, pour simplifier les calculs, que le tore est mince de sorte que le champ magnétique soit uniforme (\(r \approx R\)). Le flux à travers la bobine devient :
\(\phi = n\frac{{\mu Ni}}{{2\pi }}\frac{1}{R}\pi a^2\)
Soit :
\(M = \frac{{\mu _0 Nna^2 }}{{2R}}\)