Étude d'un circuit RLC - Impédances
Remarque : Intérêt des courants sinusoïdaux
Exemples de tensions sinusoïdales : tension du secteur (50 Hz – 220 V) – Les lignes à haute tension – L'émission et la réception des signaux de radio et de télévision font intervenir des courants qui varient sinusoïdalement dans le temps, ....
Analyse de Fourier : elle montre que toute tension périodique est une somme de fonctions sinusoïdales ; ainsi, si on sait comment réagit un circuit à une excitation sinusoïdale, alors on connaîtra (par superposition) la réponse de ce circuit à n'importe quelle tension périodique.
Fondamental : Intensité dans un circuit RLC série
L'équation différentielle du circuit (RLC) est (voir cours sur les régimes transitoires) :
\({u_L} + {u_R} + {u_C} = L\frac{{di}}{{dt}} + Ri + \frac{1}{C}q = e(t)\)
Notations :
\(e(t) = {E_m}\cos \omega t = {E_{eff}}\sqrt 2 \cos \omega t\)
L'intensité \(i(t)\) possède (une fois le régime transitoire disparu) la même pulsation que l'excitation (le GBF) :
\(i(t) = {I_m}\cos (\omega t + \varphi ) = {I_{eff}}\sqrt 2 \cos (\omega t + \varphi )\)
où \(\varphi\) est le déphasage de \(i(t)\) par rapport à \(e(t)\).
On rappelle que (voir fiche expérimentale sur les mesures de déphasage) :
\(\varphi >0\) : \(i(t)\) est en avance sur \(e(t)\).
\(\varphi>0\) : \(i(t)\) est en retard sur \(e(t)\).
Il est toujours positif d'être en avance !

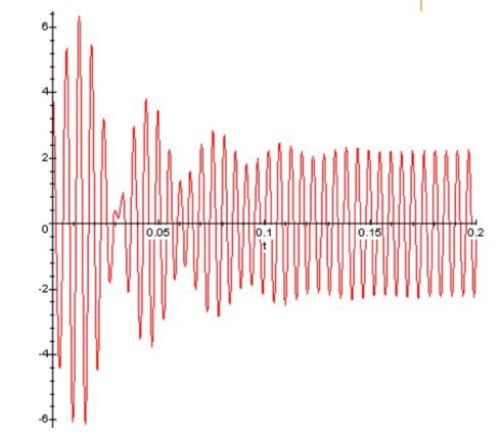
La figure suivante donne, par résolution numérique de l'équation :
\(\frac{{{d^2}{u_C}}}{{d{t^2}}} + 2\sigma {\omega _0}\frac{{d{u_C}}}{{dt}} + {\omega _0}^2{u_C} = {\omega _0}^2{E_m}\cos \omega t\)
l'allure de la tension \(u_C\) aux bornes du condensateur.
On voit l’apparition du régime permanent sinusoïdal après disparation du régime transitoire.
« Résolution » du circuit série (RLC) en notation complexe :
L'écriture de la loi des mailles dans le circuit série RLC, en notation complexe et en utilisant la notion d'impédances :
\({\underline u _R} + {\underline u _L} + {\underline u _C} = R\underline i + jL\omega \;\underline i + \frac{1}{{jC\omega }}\underline i = \underline e\)
D'où :
\(\underline i = \frac{{\underline e }}{{R + jL\omega + \frac{1}{{jC\omega }}}} = \frac{{\underline e }}{{R + j\left( {L\omega - \frac{1}{{C\omega }}} \right)}}\)
Ou encore :
\(\underline i = \frac{{\underline e }}{{\underline z }}\;\;\;\;avec\;\;\;\;\underline z = R + j\left( {L\omega - \frac{1}{{C\omega }}} \right)\)
où \(\underline z\) est l'impédance du circuit série (RLC), somme des impédances de chacun de ses constituants.
On rappelle les notations :
\(\underline i = {I_m}{e^{j(\omega t + \varphi )}}\;\;\;\;et\;\;\;\;\;\;\;\underline e = {E_m}{e^{j\omega t}}\)
Ainsi :
\({I_m}{e^{j(\omega t + \varphi )}} = \frac{{{E_m}{e^{j\omega t}}}}{{R + j\left( {L\omega - \frac{1}{{C\omega }}} \right)}}\;\;\;\;\;soit\;\;\;\;\;{I_m}{e^{j\varphi }} = \frac{{{E_m}}}{{R + j\left( {L\omega - \frac{1}{{C\omega }}} \right)}}\)
Si on note :
\(\underline z = R + j\left( {L\omega - \frac{1}{{C\omega }}} \right) = \left| {\underline z } \right|{e^{j\theta }} = Z{e^{j\theta }}\)
Alors :
\({I_m}{e^{j\varphi }} = \frac{{{E_m}}}{{Z{e^{j\theta }}}} = \frac{{{E_m}}}{Z}{e^{ - j\theta }}\;\;\;\;\;soit\;\;\;\;\;\varphi = - \theta \;\;\;\;et\;\;\;\;{I_m} = \frac{{{E_m}}}{Z}\)
L'intensité maximale vaut donc :
\({I_m} = \frac{{{E_m}}}{{\sqrt {{R^2} + {{\left( {L\omega - \frac{1}{{C\omega }}} \right)}^2}} }}\)
L'argument \(\theta\) de l'impédance complexe \(\underline z\) vérifie :
\(\cos \theta = \frac{R}{Z}\;\;\;;\;\;\;\sin \theta = \frac{{L\omega - \frac{1}{{C\omega }}}}{Z}\;\;\;;\;\;\;\tan \theta = \frac{{L\omega - \frac{1}{{C\omega }}}}{R}\)
Le déphasage \(\varphi=-\theta\) est donc connu par les relations :
\(\tan \varphi = - \frac{{L\omega - \frac{1}{{C\omega }}}}{R}\;\;\;\;et\;\;\;\;\cos \varphi = \cos \theta > 0\)
On pose \(\omega_0=1/\sqrt{LC}\) la pulsation pour laquelle \(\varphi=0\) (\(e(t)\) et \(i(t)\) sont en phase) :
Si \(\omega<\omega_0\) : le circuit est capacitif et \(\varphi>0\) (\(i(t)\) est en avance sur \(e(t)\)).
Si \(\omega>\omega_0\) : le circuit est inductif et \(\varphi<0\) (\(i(t)\) est en retard sur \(e(t)\), on retrouve bien l'effet de la loi de Lenz).
Pour \(\omega=\omega_0\) : il y a résonance d'intensité. L'intensité \(I_m\) est alors maximale et vaut :
\(I_m=\frac{E_m}{R}\)
Méthode : « Résoudre » un circuit en régime sinusoïdal
En notation complexe, on peut écrire :
Aux bornes d'un dipôle d'impédance \(\underline z\) (d'admittance \(\underline y\)) :
\(\underline u = \underline z \underline i \;\;\;\;ou\;\;\;\;\underline i = \underline y \underline u\)
Aux bornes d'un générateur de fém complexe \(\underline e\) et d'impédance interne complexe \(\underline z_G\) :
\(\underline u_G=\underline e - \underline z_G \underline i\)
Aux bornes d'un générateur de courant de courant de court-circuit \(\underline i_{cc}\) et d'admittance interne complexe \(\underline y_G\) :
\(\underline i = \underline i_{cc}-\underline y_G \underline u\)
Ainsi, on obtient pour un réseau linéaire en régime sinusoïdal forcé, des expressions identiques à celles obtenues en régime continu.
Les impédances (et admittances) prennent la place des résistances (et des conductances).
On pourra utiliser :
Les lois de Kirchhoff (loi des nœuds et des mailles), les règles des diviseurs de tension et de courant, les associations série et parallèle de dipôles, les passages de représentations de Thévenin à celle de Norton.
Complément : Les valeurs moyennes et valeurs efficaces
La valeur moyenne de l'intensité d'un courant électrique est :
\({I_{moy}} = \left\langle {i(t)} \right\rangle = \frac{1}{T}\int_0^T {i(t)dt} = \frac{Q}{T}\)
L'intensité efficace est par définition :
\({I^2}_{eff} = \left\langle {{i^2}(t)} \right\rangle = \frac{1}{T}\int_0^T {{i^2}(t)dt}\)
L'intensité efficace est l'intensité d'un courant continu qui dissiperait dans une résistance R, en une période, la même énergie que le courant alternatif :
\(P = \int_0^T {R{i^2}(t)dt} = RI_{eff}^2T\)
On prend l'exemple d'un courant en dents de scie : on considère \(i(t)\) donnée par la courbe ci-dessous.
Calculer l'intensité moyenne et l'intensité efficace de ce courant en dents de scie.
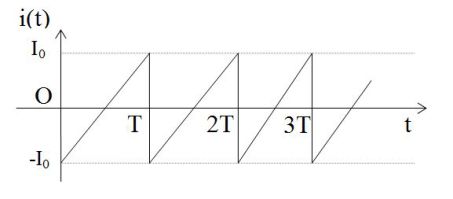
On trouve :
\(I_{moy}=0\)
Et :
\(I_{eff}=\frac{I_0}{\sqrt{3}}\)
On rappelle que, pour un courant sinusoïdal \(i(t)=I_mcos\omega t\) :
\(I_{moy}=0\)
Et :
\(I_{eff}=\frac{I_m}{\sqrt{2}}\)