Interfaces between two medium
Fondamental : Dielectrics
In the matter, an electromagnetic field acts on the atoms, molecules or ions by deforming them. The material medium is as follows :
Polarize under the influence of the electric field.
Magnetize under the action of the magnetic field.
In some mediums (metal, plasmas), the charges move freely (we talk about free charges and currents).
In dielectric (or insulating) the charges do move only very little and are organized mainly in the form of electric dipoles (neglecting the contributions due to the apparition of quadrupole or even electric octopoles).
These changes will then cause the apparition of an electric field (or magnetic) induced by the external electromagnetic field, which is added thereto.
One mistake is to believe that an insulating medium (such as dielectric) does not let the waves pass through (radio for example).
This is exactly the opposite : the dielectrics are essentially transparent to radio waves, while conductor medium (sea water, metals) reflect and absorb them.
.
Fondamental : Speed of an electromagnetic wave in a dielectric
We define the index \(n\) of a dielectric medium (such as glass, for example), in the form :
\(n=\frac{c}{v}\)
Where \(c\) is the speed of light in vacuum and \(v\) the velocity of light in the medium under consideration.
For glass, \(n\) is about \(1,6\) and for water, \(n\) is about \(1,3\).
Vacuum has an index equal to \(1\) and the air was very close to that of vacum index.
D'Alembert's equations for electromagnetic fields then become, replacing \(v\) by \(c/n\) :
\(\Delta \underline {\vec E} - \frac{{{n^2}}}{{{c^2}}}\frac{{{\partial ^2}\underline {\vec E} }}{{\partial {t^2}}} = \vec 0\;\;\;\;\;\;\;\;\;\;;\;\;\;\;\;\;\;\;\;\;\Delta \underline {\vec B} - \frac{{{n^2}}}{{{c^2}}}\frac{{{\partial ^2}\underline {\vec B} }}{{\partial {t^2}}} = \vec 0\)
Fondamental : Reflection and transmission coefficients (in amplitude)
Reflection and refraction of electromagnetic waves : reflection and transmission coefficients (in amplitude) at normal incidence
Consider two dielectric mediums \((1)\) and \((2)\).
It is located in the transparent areas for which the index of the two medium \(n_1\) and \(n_2\) are real.
An incident wave reaches the interface between the two medium (onto the interface surface between the two dielectric) at normal incidence.
We wish to determine reflected wave and transmitted wave.
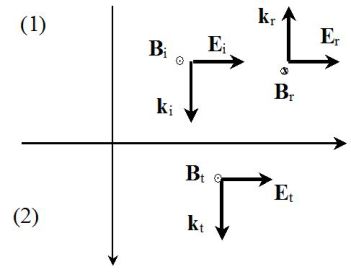
The polarized waves is assumed linearly :
Note the wave vectors (\(k_0=\omega/c\) is the wave vector in vacuum) :
\(\vec k_i = (\omega/v_1) \;\vec u_z=n_1 (\omega/c) \;\vec u_z = n_1k_0\; \vec u_z\)
Also :
\(\vec k_r = -n_1k_0 \;\vec u_z\)
\(\vec k_t = n_2k_0 \;\vec u_z\)
Expressions of electric fields :
\(\underline {\vec E}_i=E_{0i} e^{i(\omega t-n_1k_0z)}\;\vec u_x\)
\(\underline {\vec E}_r=E_{0r} e^{i(\omega t+n_1k_0z)}\;\vec u_x\)
\(\underline {\vec E}_t=E_{0t} e^{i(\omega t-n_2k_0z)}\;\vec u_x\)
Expression of magnetic fields :
One obtains the magnetic fields using the relation of the structure of a plane wave.
So :
\(\underline {\vec B}_i=\frac{\vec u_z }{v_1}\wedge \underline {\vec E}_i=n_1\frac{\vec u_z }{c}\wedge \underline {\vec E}_i\)
Or, finally :
\(\underline {\vec B}_i=n_1\frac{E_{0i} }{c}e^{i(\omega t-n_1k_0z)}\;\vec u_y\)
Similarly (the reflected wave propagates in \(-\vec u_z\)) :
\(\underline {\vec B}_r=-n_1\frac{E_{0r} }{c}e^{i(\omega t+n_1k_0z)}\;\vec u_y\)
And :
\(\underline {\vec B}_t=n_2\frac{E_{0t} }{c}e^{i(\omega t-n_2k_0z)}\;\vec u_y\)
Dielectrics are uncharged. In a volumetric representation, there is continuity of the electric and magnetic fields at the crossing in the diopter at \(z=0\).
Therefore, the boundary conditions for the fields are written :
For the electric field :
\(E_{0i}+E_{0r}=E_{0t}\)
For the magnetic field :
\(n_1E_{0i}-n_1E_{0r}=n_2E_{0t}\)
We can deduce :
\({E_{0r}} = r{E_{0i}}\;\;\;\;\;\;\;\;\;\;\;with\;\;\;\;\;\;\;\;\;r = \frac{{{n_1} - {n_2}}}{{{n_1} + {n_2}}}\)
\(r\) is the amplitude reflection coefficient for the electric field.
And :
\({E_{0t}} = t{E_{0i}}\;\;\;\;\;\;\;\;\;\;\;with\;\;\;\;\;\;\;\;\;t = \frac{{2{n_1}}}{{{n_1} + {n_2}}}\)
\(t\) is the amplitude transmission coefficient for the electric field.
Some notes :
\(t\) is always positive : there is no phase change during transmission.
\(r\) can be positive or negative :
\(n_1>n_2\) : reflection introduces no phase shift
\(n_1<n_2\) : reflection introduces a phase shift equals to \(\pi\).
Fondamental : Reflection and transmission coefficients (in energy)
The incident Poynting vector is (on average) :
\(\left\langle {{{\vec \Pi }_i}} \right\rangle = \frac{{{n_1}}}{{2{\mu _0}c}}E_{0,i}^2\;{\vec u_x}\)
For reflected and transmitted waves :
\(\left\langle {{{\vec \Pi }_r}} \right\rangle = \frac{{{n_1}}}{{2{\mu _0}c}}E_{0,r}^2\;( - {\vec u_x})\;\;\;\;\;\;\;\;\;\;and\;\;\;\;\;\;\;\;\;\;\;\;\left\langle {{{\vec \Pi }_t}} \right\rangle = \frac{{{n_2}}}{{2{\mu _0}c}}E_{0,t}^2\;{\vec u_x}\)
The coefficients in energy of reflection and transmission wave are then :
\(R = \frac{{\left\langle {{{\vec \Pi }_r}} \right\rangle }}{{\left\langle {{{\vec \Pi }_i}} \right\rangle }} = {r^2} = {\left( {\frac{{{n_1} - {n_2}}}{{{n_1} + {n_2}}}} \right)^2}\;\;\;\;\;\;\;\;\;\;and\;\;\;\;\;\;\;\;\;\;T = \frac{{\left\langle {{{\vec \Pi }_t}} \right\rangle }}{{\left\langle {{{\vec \Pi }_i}} \right\rangle }} = \frac{{{n_2}}}{{{n_1}}}{t^2} = \frac{{4{n_1}{n_2}}}{{{{({n_1} + {n_2})}^2}}}\)
We verify the conservation of energy :
\(R+T=1\)
A numerical application :
In the case of the diopter air-glass (\(n_1\approx 1\) and \(n_2=1,5\)) :
\(R=0,04\) and \(T=0,96\) : practically, energy is completely transmitted.