Black holes
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
A black hole is a body so dense that no light or matter can espace from inside it.
The following exercice explains the classical description that Laplace could have had of black holes.
Question
Laplace's star : in \(1798\), in «Exposition du système du Monde», Laplace thought of a star (with spherical mass repartition) the same density of the Earth (\(\rho_T\)) and of radius equal to \(250\) times the one of the Sun.
What is the corresponding escape velocity \(v_{lib}\) on the surface of the star ?
Data :
Distance Earth - Sun : \(d=1,5.10^{11}m\)
Mass and radius of the Earth : \(M_T=6.10^{24}\;kg\) and \(R_T=6,4.10^6\;m\)
Mass and radius of the Sun : \(M_S=2.10^{30}\;kg\) and \(R_S=7.10^8\;m\)
Gravitational Constant : \(G=6,67.10^{-11}\;SI\)
Solution
Escape velocity is defined as the minimal velocity (in the « astrocentric » reference frame) to give to a material point of mass \(m\) for it to escape the gravitational pull of the star.
In this reference frame (which we suppose to be inertial), the mechanical energy of a material point is (if we suppose only the conservative gravitational force of the star is applied to it) :
\(E_m=\frac{1}{2}mv^2-\frac{GmM}{r}\)
On the surface of the star, it is : (\(R\) and \(M\) are the radius and the mass of the star)
\(E_m=\frac{1}{2}mv_{lib}^2-GmM\frac{1}{R}\)
When the point escapes the gravitational pull of the star, its potential energy and its kinetic energy are equal to zero. Its mechanical energy is also zero, thus :
\(E_m=\frac{1}{2}mv_{lib}^2-GmM\frac{1}{R}=0\)
So :
\(v_{lib}=\sqrt{\frac{2GM}{R}}\)
We write the masses as :
\(M = (4/3)\pi {R^3}{\rho _T}\) and \({M_T} = (4/3)\pi R_T^3{\rho _T}\), \(M = {(R/{R_T})^3}{M_T}\)
Thus :
\({v_{lib}} = \sqrt {\frac{{2G{M_T}}}{R}{{\left( {\frac{R}{{{R_T}}}} \right)}^3}}\)
Numerical application :
\(R = 250\,{R_S} = {1,75.10^{11}}m\) and \({v_{lib}} = {3,06.10^8}\;m.{s^{ - 1}} > c\).
Laplace concluded that such a star cannot let light escape its surface, thus making it invisible.
In general relativity, such an « object » is nowadays called a « black hole ».
Question
Schwarzschild radius : a body of mass \(M\) is a black hole if its radius \(R\) is smaller than a critical radius \(R_C\), called Schwarzschild radius.
Escape velocity on the surface of a body with radius \(R_C\) is equal to the speed of light in a vacuum : \(v_{lib}=c\).
Give \(R_C\) using \(G\), \(M\) and \(c\).
Numerical application : give \(R_C\) for the Sun, then for the Earth.
Give the gravitational force \(F_{TN}\) exerted by a black hole on an object P using the mass of the objet \(m\), the distance between this object and the center of the black hole \(r\), the critical radius of the black hole \(R_C\) and \(c\).
Calculate \(F_{TN}\) if : \(R_C=8,9\;mm\;\; ;\;\; m=3\;kg\;\; ;\;\; r=6\;400\;km\)
Calculate the gravitational field \(g_{TN}\) on the surface of the Schwarzschild sphere, using \(R_C\) and \(c\).
Numerical application : give \(g_{TN}\) if \(R_C=8,9\;mm\).
Why is this sphere of radius \(R_C\) called « event horizon » ?
Solution
Escape velocity is \( c\) if the radius is \(R_C\) :
\(c = \sqrt {2GM/{R_c}}\) so \({R_c} = 2GM/{c^2}\)
Numerically :
\(R_C=3\;km\) for the Sun and \(R_C=8,9\;mm\) for the Earth.
The gravitational pull exerted by the black-hole on the point P is :
\({F_{TN}} = GmM/{r^2}\)
Or :
\(GM = {c^2}{R_c}/2\)
Thus :
\({F_{TN}} = m{c^2}{R_c}/2{r^2}\)
Numerically :
\(F_{TN}=29,4\;N\)
This is the weight of an object placed on the surface of the Earth, since the Earth's radius is equal to the distance between P and the center of the black hole.
The gravitational field on the surface is :
\({g_{TN}} = GM/R_c^2\)
So :
\({g_{TN}} = {c^2}/2{R_c} = {5,1.10^{18}}\;m.{s^{ - 2}}\)
It is huge : it is the field created by an object which has the same mass as the Earth, but contained in the volume of a small marble !
The interior of the Schwarzschild sphere (radius \(R_C\)) is the critical volume from which light cannot escape.
Light received by an exterior observer is at best emitted by the surface of the sphere, hence the name « event horizon ».
Question
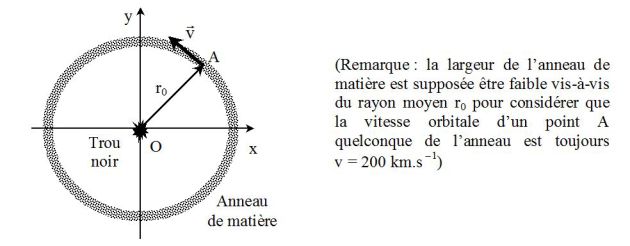
Application : at the center of our galaxy
Astronomes observed a small object at the center of our galaxy, around which orbits a ring of mater.
This ring has a diameter of \(15\) \(ly\) (\(ly= light \;year\), the distance that travels light in a vacuum in a year) and its orbital velocity is about \(v=200\;km.s^{-1}\).
Give the mass \(M_{OM}\) of this object, in \(kg\) and in solar mass unit.
We will suppose the mass of the object to be far superior to the one of the ring.
Most astronomers think this massive object is actually a black hole.
Calculate its Schwarzschild radius. Compare it to the numerical value of the distance \(d\) between the Earth and the Sun.
Data :
Distance Earth - Sun : \(d=1,5.10^{11}m\)
Solution
The reference frame is the one of the massive body, centered in O (same as the barycentric reference frame).
The second law of motion for a particle A in the ring of matter, having a circular motion of radius \(r_0\) and velocity \(v\) around the black hole (see figure) is, when projected along OA :
\(m\frac{{{v^2}}}{{{r_0}}} = \frac{{Gm{M_{OM}}}}{{r_0^2}}\)
So :
\({M_{OM}} = \frac{{{r_0}{v^2}}}{G}\)
Numerically, with \({r_0} = 7,5\,ly\; = \;{7,1.10^{16}}\;m\), \({M_{OM}} = {4,26.10^{37}}\;kg = {2,13.10^7}\;{M_S}\), more than \(20\) millions times the mass of the Sun !
The Schwarzschild radius of the black hole is : \({R_c} = 2GM/{c^2} = {6,3.10^{10}}\;m\), which is \(63\) millions of kilometers, or \(42\)% of the distance between the Earth and the Sun.
Such gigantic black holes have a mass of millions of solar mass and they are very dense.
They could be at the center of many galaxies.